以下均不会过多介绍算法,主要介绍的是做题的思维。
PART-1
最小生成树
最小生成树主要用于解决使用最小边权和的边连接后让图连通。
如果有负权边,则视题目意思而定。
1、普通使用
例题:
在一个 $n \times m$ 的矩形区域内,外围边界存在围墙,每个 $1 \times 1$ 的正方形区域内也存在对角线方向的一堵墙,墙的方向有两种,如下图所示:

对角线方向的墙可以破坏,不同的墙破坏的代价不同。
支付最少的代价破坏墙,使得整个区域连通。
$1 \le n,m \le 500,1 \le w_{i,j} \le 5\times 10^3$。
很显然,每个 $1 \times 1$ 的小方格都分成了两个部分,这样我们把图建出来,然后对于有墙阻碍的边边权就是 $w$,否则边权为 $0$,一共 $n \times m$ 级别的边,所以用 Kruskal 就可以了。
2、配合倍增
P4180 [BJWC2010] 严格次小生成树
每次考虑用一条非最小生成树上的边替换最小生成树上的边,为确保次小,肯定是替换能替换的边权最大的边。
观察到非树边能够替换的边是树上两点间的路径,所以 $O(\log n)$ 用倍增或 $O(\log^2 n)$ 用树链剖分。
还有其它类似的题,套路都一样。
3、其它
例题1:
求一个包含 $n$ 个点 $m$ 条边的仙人掌的 $k$ 小生成树。
显然,每个环上选一条边,非环边全选,所以变成了一个 $k$ 路归并问题,可以做到 $O(nk \log k) \sim O(k \log k)$ 的时间复杂度。
例题2:*神仙题
Alice 和 Bob 在由 $n$ 个点 $m$ 条边构成的无向连通图上进行游戏。
对于一条连接节点 $x_i$ 与 $y_i$ 的边,其边权的可选项只有 $a_i$ 或 $b_i$ 。
游戏首先由 Alice 选择恰好 $k$ 条边,使其边权选择 $a_i$,而剩下的 $m-k$ 条边的边权选择 $b_i$。然后再由 Bob 选择恰好 $n-1$ 条边,构成原图的一棵生成树。最终的得分为 Bob 选择的生成树的边权之和。
Alice 想让得分尽量大,而 Bob 想让得分尽量小。在双方都按最佳策略行动时,最终的得分为多少?请你分别计算 $k=0\sim m$ 时的答案。
$1 \le n \le 9,1 \le m \le 30,1 \le T \le 20$,不含重边和自环。
对于 $m$ 不好维护,考虑对 $n$ 进行处理。
由题得 Bob 其实就是求最小生成树,别无选择,真正有选择权的是 Alice。
考虑 Kruskal 的执行过程,对边排序之后能选就选。
那么我们在这道题中把 $a_i$ 和 $b_i$ 拆开排序,然后对于每个决策点设 $dp_{i,j,S}$ 表示枚举到了第 $i$ 条边,选了 $j$ 条 $a_i$ 的边(相同顶点的边一定不会重复选,所以不用担心计算重复),当前并查集的状态为 $S$ 时候最小生成树最大是多少。
记录了并查集的状态后,本题就很好做了,因为 $Bell_9$ 大概在 $2 \times 10^4 \sim 3\times 10^4$ 之间,所以时间空间都不是问题。
最小树形图
给定 $n$ 个点 $m$ 条边的有向图,求出其边权和最小的一个子图,满足其是一棵外向树(所有边都是父亲指向儿子)。
下面有两种算法解决这个问题,但它们无一例外都无法较好地解决输出方案的问题,输出方案需要扩展过程中缩的环,并且一般不会被用到,这里就不再赘述了。
朱刘算法 & Tarjan 的优化
下面先给出普通的朱刘算法的简介,即在 $O(nm)$ 的时间内求出这个问题的答案。
设根节点为 $r$,则在初始的时候维护一个栈,设栈顶是 $s_t$,栈底是 $s_1$,那么就相当于维护了 $s_t \to s_{t-1},s_{t-1} \to s_{t-2},\dots,s_2\to s_1$ 这一条链。
每次找到栈顶 $s_t$,以及指向它的一条边权最短的边 $u \to s_t$,如果 $u \in s_{1 \sim t}$,设 $u=s_p$,那么 $s_p,s_{p+1},\dots,s_t$ 形成了一个环,我们把这个环缩成一个点即可;否则直接将 $s_{t+1} \gets u$ 即可。
最后为了确保图的连通性,我们可以将 $1 \to 2,2 \to 3,\dots,n \to 1$ 连向 $\text{inf}$ 的边,这样的话如果最终的答案 $\ge \text{inf}$,那么就代表不存在任何一棵最小树形图。
接下来我们需要考虑边权的问题,OI-wiki 上写得太简略了,这里补充一下,证明倒可以参考一下 OI-wiki。
首先找到了 $u$,如果 $u \not\in s$,那么直接加入,此处不统计边权;如果 $u$ 和某些点形成了环,那么我们需要加上这个环所有边的边权,并且把这个环缩点,设 $E_u$ 表示以 $u$ 为终点的边的集合,那么相当于答案加上所有 $id \in s_{p \sim t},\min_{i \in E_{id}}{val_i}$。
因为后面答案可能会反悔,也就是不选这条边,设 $\min_{i \in E_{id}}{val_i}$ 为 $Emin_{u}$,那么我们需要将 $Emin_u$ 从 $E_u$ 中删去,并且支持反悔,就将 $E_u$ 内剩下边的权值减去我们选出来的边的权值就可以了。
合并和全部减一个树,还要找最小值,于是我们直接使用左偏树即可。
特别的,如果 $u$ 与根节点(合并)在同一个集合,那么答案不能累加上 $Emin_u$,因为根节点是没有入边的。
注意:尽管链的方向是向内的,但是我们强制规定了根节点没有入边,其它节点都有入边,所以这棵树实际上是向外扩展的,如果我们真的要求内向树,那么把边反向即可。
代码如下,以 P4716 【模板】最小树形图 为例:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
| #include<bits/stdc++.h>
#define ll long long
#define N 500005
#define inf 100000000000000ll
using namespace std;
struct node{ll id,x,tag;}p[N];
struct tree{ll cnt,x,tag;}tr[N<<2];
vector<ll> op[N],w[N];
ll n,m,q,sums,a[N],i,x,y,z,ls[N],rs[N],dist[N],root[N],tot,lis[N],top,aroot,fath[N],toped[N],dfn[N],nid[N],tot_dfn,vis[N],idd,sum[N],son[N],f[N];
char ch;
inline ll gf(ll x){return x==f[x]?x:f[x]=gf(f[x]);}
inline void pushtag_heap(ll id,ll c){if(id) p[id].x+=c,p[id].tag+=c;}
inline void pushdown_heap(ll id){pushtag_heap(ls[id],p[id].tag),pushtag_heap(rs[id],p[id].tag),p[id].tag=0;}
inline ll merge(ll x,ll y){
if(!x||!y) return x+y;
pushdown_heap(x),pushdown_heap(y);
if(p[x].x>p[y].x) swap(x,y);
rs[x]=merge(rs[x],y);
if(dist[ls[x]]<dist[rs[x]]||(dist[ls[x]]==dist[rs[x]]&&ls[x]>rs[x])) swap(ls[x],rs[x]);
dist[x]=dist[rs[x]]+1;
return x;
}
inline void pop(ll p){pushdown_heap(root[p]),root[p] = merge(ls[root[p]],rs[root[p]]);}
inline void pushup(ll p){
tr[p].cnt = min(tr[2*p].cnt,tr[2*p+1].cnt),tr[p].x = 0;
if(tr[2*p].cnt==tr[p].cnt) tr[p].x+=tr[2*p].x;
if(tr[2*p+1].cnt==tr[p].cnt) tr[p].x+=tr[2*p+1].x;
}
inline void pushtag(ll p,ll c){tr[p].cnt+=c,tr[p].tag+=c;}
inline void pushdown(ll p){if(tr[p].tag) pushtag(2*p,tr[p].tag),pushtag(2*p+1,tr[p].tag),tr[p].tag=0;}
inline void build(ll s,ll t,ll p){
if(s==t){
tr[p].x = a[nid[s]];
return ;
}
build(s,(s+t)/2,2*p),build((s+t)/2+1,t,2*p+1);
pushup(p);
}
inline void modify(ll l,ll r,ll c,ll s,ll t,ll p){
if(l<=s&&t<=r) return pushtag(p,c);
pushdown(p);
if(l<=(s+t)/2) modify(l,r,c,s,(s+t)/2,2*p);
if(r>(s+t)/2) modify(l,r,c,(s+t)/2+1,t,2*p+1);
pushup(p);
}
inline void to_root(ll p,ll c){while(p) modify(dfn[toped[p]],dfn[p],c,1,tot_dfn,1),p=fath[toped[p]];}
inline void dfs1(ll x){
sum[x]=1;
for(ll i=0;i<op[x].size();i++){
if(op[x][i]==fath[x]) continue;
fath[op[x][i]] = x;
dfs1(op[x][i]);
sum[x] += sum[op[x][i]];
if(sum[son[x]]<sum[op[x][i]]) son[x]=op[x][i];
}
}
inline void dfs2(ll x,ll top){
toped[x] = top,dfn[x] = ++tot_dfn,nid[tot_dfn] = x;
if(son[x]) dfs2(son[x],top);
for(ll i=0;i<op[x].size();i++){
if(op[x][i]==fath[x]||op[x][i]==son[x]) continue;
dfs2(op[x][i],op[x][i]);
}
}
int main(){
ios::sync_with_stdio(false);
cin>>n>>m>>q;
idd=n;
for(i=1;i<=m;i++){
cin>>x>>y>>z;
p[++tot] = (node){x,z,0};
root[y] = merge(root[y],tot);
}
for(i=1;i<=n;i++) p[++tot] = (node){i%n+1,inf},root[i] = merge(root[i],tot),f[i]=i;
lis[++top] = q,vis[q] = 1;
while(1){
ll u = lis[top];
while(root[u]&&gf(p[root[u]].id)==gf(u)) pop(u);
if(!root[u]) break;
ll pos = gf(p[root[u]].id),val = p[root[u]].x;
if(!vis[pos]){
vis[pos]=1,lis[++top]=pos;
continue;
}
idd++,f[idd]=idd;
while(lis[top+1]!=pos){
ll now = lis[top--],val = p[root[now]].x,fro = p[root[now]].id;
vis[now]=0,pushtag_heap(root[now],-val),pop(now);
if(gf(now)!=gf(q)) sums+=val;
root[idd]=merge(root[idd],root[now]),f[now]=idd;
}
vis[idd]=1,lis[++top]=idd;
}
if(sums<1e9) cout<<sums<<endl;
else cout<<"-1\n";
return 0;
}
|
因为用了左偏树合并,所以时间复杂度优化到了 $O(m+n \log n)$。
构造
接下来我们以 CF240E Road Repairs 来介绍一下如何利用 Tarjan 优化输出方案。(这道题是外向树,因此下面以外向树为例)
考虑朱刘算法的本质,就是先找到一个环,这个环上的边先放到待选集合内,当然,入点是根节点所在环除外,因为根节点不可能作为入点出现。
每次缩点的时候,如果我们在另外的图上将新建的点向环上的点连边,那么就形成了一棵“收缩树”,这棵树的形态如下所示,左边是原图,右边是建立出来的收缩树:
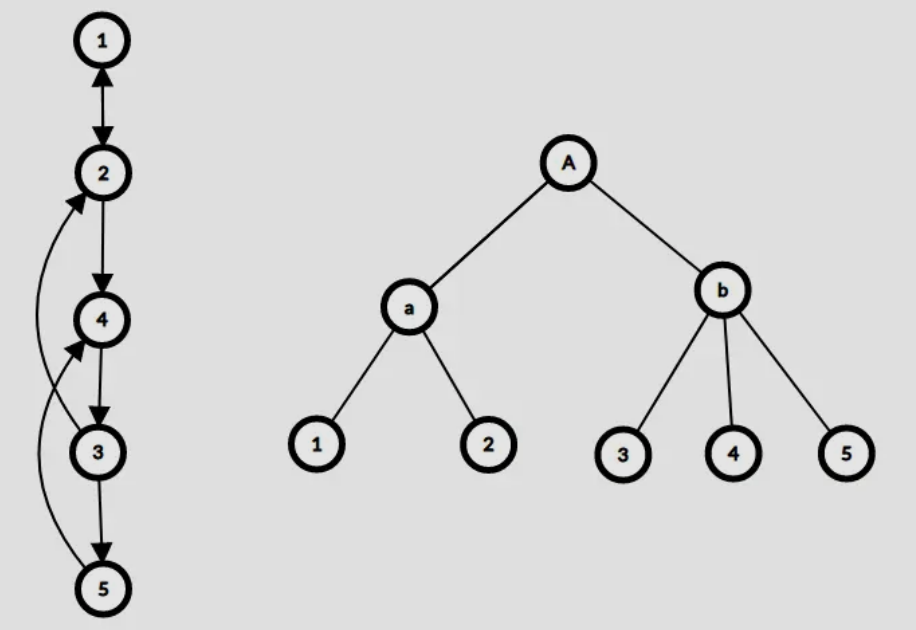
因为加边是有顺序的,但是我们仍然不能使用并查集来判断,因为这是有向图,所以我们可以在过程中累加过答案的边加进去,然后从根开始遍历一棵合法的最小树形图就可以了。
这样做的正确性在于我们考虑一下收缩树,每次从根节点开始访问,根节点一定是最后一个合并的节点,它访问到的边就是最后合并的边,而根据反悔贪心的优先性,我们肯定是从最后合并的边开始选,然后不能加进答案就代表被反悔了。
但是这是深度优先搜索,也就是说也有可能在访问一棵子树的时候通过一条本来被反悔的边访问到另外的子树,想一下,这样是不可能的,因为如果有这样的边,那么这两棵子树所代表的环一定是合并了的,并不会影响答案。
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
| #include<bits/stdc++.h>
#define ll long long
#define N 500005
#define inf 100000000000000ll
using namespace std;
struct node{ll id,x,tag,idd,beg;}p[N];
vector<pair<ll,ll> > op[N];
ll n,m,q,sums,a[N],i,x,y,z,ls[N],rs[N],dist[N],root[N],tot,lis[N],top,aroot,vis[N],idd,sum[N],son[N],f[N],chose[N];
ll ex[N],ey[N],ez[N],toped,vall[N];
char ch;
inline ll gf(ll x){return x==f[x]?x:f[x]=gf(f[x]);}
inline void pushtag_heap(ll id,ll c){if(id) p[id].x+=c,p[id].tag+=c;}
inline void pushdown_heap(ll id){pushtag_heap(ls[id],p[id].tag),pushtag_heap(rs[id],p[id].tag),p[id].tag=0;}
inline ll merge(ll x,ll y){
if(!x||!y) return x+y;
pushdown_heap(x),pushdown_heap(y);
if(p[x].x>p[y].x) swap(x,y);
rs[x]=merge(rs[x],y);
if(dist[ls[x]]<dist[rs[x]]||(dist[ls[x]]==dist[rs[x]]&&ls[x]>rs[x])) swap(ls[x],rs[x]);
dist[x]=dist[rs[x]]+1;
return x;
}
inline void pop(ll p){pushdown_heap(root[p]),root[p] = merge(ls[root[p]],rs[root[p]]);}
inline void dfs(ll x){
f[x]=1;
for(ll i=0;i<op[x].size();i++){
if(f[op[x][i].first]) continue;
chose[op[x][i].second]=1;
dfs(op[x][i].first);
}
}
int main(){
freopen("input.txt","r",stdin);
freopen("output.txt","w",stdout);
ios::sync_with_stdio(false);
cin>>n>>m,idd=n;
for(i=1;i<=m;i++){
cin>>x>>y>>z,vall[i]=z;
p[++tot] = (node){x,z,0,i,y};
root[y] = merge(root[y],tot);
}
for(i=1;i<=n;i++) p[++tot] = (node){i%n+1,inf,0,-1,i},root[i] = merge(root[i],tot),f[i]=i;
lis[++top] = 1,vis[1] = 1;
while(1){
ll u = lis[top];
while(root[u]&&gf(p[root[u]].id)==gf(u)) pop(u);
if(!root[u]) break;
ll pos = gf(p[root[u]].id);
if(!vis[pos]){
vis[pos]=1,lis[++top]=pos;
continue;
}
idd++,f[idd]=idd;
while(lis[top+1]!=pos){
ll now = lis[top--],val = p[root[now]].x,fro = p[root[now]].id,to = p[root[now]].beg,zz = p[root[now]].idd;
vis[now]=0,pushtag_heap(root[now],-val),pop(now);
if(gf(now)!=gf(1)) sums+=val,toped++,ex[toped]=fro,ey[toped]=to,ez[toped]=zz;
root[idd]=merge(root[idd],root[now]),f[now]=idd;
}
vis[idd]=1,lis[++top]=idd;
}
if(sums<1e9){
cout<<sums<<endl;
for(i=1;i<=n;i++) f[i]=0;
for(i=1;i<=toped;i++) op[ex[i]].push_back(make_pair(ey[i],ez[i]));
dfs(1);
for(i=1;i<=m;i++) if(chose[i]&&vall[i]) cout<<i<<" ";
cout<<endl;
}
else cout<<"-1\n";
return 0;
}
|
应用
CF 1870H Standard Graph Problem
如果是无向图,那么答案一定是最小生成树的一个边集,这里感性证明一下就好。
如果是一棵内向树,那么如果 $i$ 被选中,那么 $i$ 往根的路径上的边都不需要选,直接用线段树的树链剖分和维护最小值的和即可。
如果不是内向树,通过上面的朱刘算法+Tarjan 优化转化成内向树就可以了,这个贪心也是感性证明一下就好。
代码如下,时间复杂度双 $\log$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
| #include<bits/stdc++.h>
#define ll long long
#define N 500005
#define inf 100000000000000ll
using namespace std;
struct node{ll id,x,tag;}p[N];
struct tree{ll cnt,x,tag;}tr[N<<2];
vector<ll> op[N],w[N];
ll n,m,q,sums,a[N],i,x,y,z,ls[N],rs[N],dist[N],root[N],tot,lis[N],top,aroot,fath[N],toped[N],dfn[N],nid[N],tot_dfn,vis[N],idd,sum[N],son[N],f[N];
char ch;
inline ll gf(ll x){return x==f[x]?x:f[x]=gf(f[x]);}
inline void pushtag_heap(ll id,ll c){if(id) p[id].x+=c,p[id].tag+=c;}
inline void pushdown_heap(ll id){pushtag_heap(ls[id],p[id].tag),pushtag_heap(rs[id],p[id].tag),p[id].tag=0;}
inline ll merge(ll x,ll y){
if(!x||!y) return x+y;
pushdown_heap(x),pushdown_heap(y);
if(p[x].x>p[y].x) swap(x,y);
rs[x]=merge(rs[x],y);
if(dist[ls[x]]<dist[rs[x]]||(dist[ls[x]]==dist[rs[x]]&&ls[x]>rs[x])) swap(ls[x],rs[x]);
dist[x]=dist[rs[x]]+1;
return x;
}
inline void pop(ll p){pushdown_heap(root[p]),root[p] = merge(ls[root[p]],rs[root[p]]);}
inline void pushup(ll p){
tr[p].cnt = min(tr[2*p].cnt,tr[2*p+1].cnt),tr[p].x = 0;
if(tr[2*p].cnt==tr[p].cnt) tr[p].x+=tr[2*p].x;
if(tr[2*p+1].cnt==tr[p].cnt) tr[p].x+=tr[2*p+1].x;
}
inline void pushtag(ll p,ll c){tr[p].cnt+=c,tr[p].tag+=c;}
inline void pushdown(ll p){if(tr[p].tag) pushtag(2*p,tr[p].tag),pushtag(2*p+1,tr[p].tag),tr[p].tag=0;}
inline void build(ll s,ll t,ll p){
if(s==t){
tr[p].x = a[nid[s]];
return ;
}
build(s,(s+t)/2,2*p),build((s+t)/2+1,t,2*p+1);
pushup(p);
}
inline void modify(ll l,ll r,ll c,ll s,ll t,ll p){
if(l<=s&&t<=r) return pushtag(p,c);
pushdown(p);
if(l<=(s+t)/2) modify(l,r,c,s,(s+t)/2,2*p);
if(r>(s+t)/2) modify(l,r,c,(s+t)/2+1,t,2*p+1);
pushup(p);
}
inline void to_root(ll p,ll c){while(p) modify(dfn[toped[p]],dfn[p],c,1,tot_dfn,1),p=fath[toped[p]];}
inline void dfs1(ll x){
sum[x]=1;
for(ll i=0;i<op[x].size();i++){
if(op[x][i]==fath[x]) continue;
fath[op[x][i]] = x;
dfs1(op[x][i]);
sum[x] += sum[op[x][i]];
if(sum[son[x]]<sum[op[x][i]]) son[x]=op[x][i];
}
}
inline void dfs2(ll x,ll top){
toped[x] = top,dfn[x] = ++tot_dfn,nid[tot_dfn] = x;
if(son[x]) dfs2(son[x],top);
for(ll i=0;i<op[x].size();i++){
if(op[x][i]==fath[x]||op[x][i]==son[x]) continue;
dfs2(op[x][i],op[x][i]);
}
}
int main(){
ios::sync_with_stdio(false);
cin>>n>>m>>q;
idd=n;
for(i=1;i<=m;i++){
cin>>x>>y>>z;
swap(x,y);
p[++tot] = (node){x,z,0};
root[y] = merge(root[y],tot);
}
for(i=1;i<=n;i++) p[++tot] = (node){i%n+1,inf},root[i] = merge(root[i],tot),f[i]=i;
lis[++top] = 1,vis[1] = 1;
while(1){
ll u = lis[top];
while(root[u]&&gf(p[root[u]].id)==gf(u)) pop(u);
if(!root[u]) break;
ll pos = gf(p[root[u]].id),val = p[root[u]].x;
if(!vis[pos]){
vis[pos]=1,lis[++top]=pos;
continue;
}
idd++,f[idd]=idd;
while(lis[top+1]!=pos){
op[idd].push_back(lis[top]),a[lis[top]]=p[root[lis[top]]].x;
ll now = lis[top--],val = p[root[now]].x,fro = p[root[now]].id;
vis[now]=0,f[now]=idd,pushtag_heap(root[now],-val),pop(now);
root[idd]=merge(root[idd],root[now]);
}
vis[idd]=1,lis[++top]=idd;
}
aroot = lis[1],a[aroot] = inf;
dfs1(aroot),dfs2(aroot,aroot),build(1,tot_dfn,1);
while(q--){
cin>>ch>>x;
if(ch=='+') to_root(x,1);
else to_root(x,-1);
if(tr[1].cnt!=0) cout<<0<<endl;
else if(tr[1].x>=inf) cout<<-1<<endl;
else cout<<tr[1].x<<endl;
}
return 0;
}
|
最短路
本节主要介绍最短路的一些小技巧。
1、虚点
例题:对于一棵有根树,两个点之间如果有边,则可以双向到达,如果没边但是深度之差等于 $k$,也可以双向到达。
问 $s$ 到 $t$ 的最短路是多少,边有边权,$1 \le k \le n \le 10^6$。
首先,对于任意两个深度满足差等于 $k$ 的点不能暴力连,因为时间空间都是 $O(n^2)$ 的。
但是我们可以对每个深度建一个虚拟节点,这个节点连向当前深度所有节点,然后满足深度之差等于 $k$ 的两个虚拟节点连边就可以了,这下子时间和空间都优化到了 $O(n)$ 级别,而且照样可以跑最短路。
2、多维
很多题目涉及到多维度的问题,例如上一条边的边权对于下一条经过的边的边权有影响,那么我们这时可以像 DP 一样多一个维度来记录。
例题:某图由 $n$ 点 $m$ 条单向边构成,每条边都有通行所需的费用 $w_i$ 。
其中某些边是特殊边,当经过特殊边从 $x_i$ 点到达 $y_i$ 点后,会触发神秘力量,可以选择使下一次的通行费用减少 $k$ ,或者直接 $0$ 费传送到某个由 $y_i$ 出发无法一步到达的点。
注意:经过一条费用减少 $k$ 后的特殊边,同样也能触发神秘力量。
计算从 $s$ 出发,到达每一个点所需的最少花费。
很显然,设 $dp_{i,0/1}$ 表示到达 $i$ 号点后上一条边是特殊边还是普通边,转移(Dijkstra)同普通最短路。
但是还有 $0$ 费传送的情况,如何处理,这个参考数据结构板块的并查集合并区间的处理方式。
3、期望
对于 $dp_i = \min{\dots}$ 的类型的题目,我们有两种解决方式,一是高斯消元 $O(n^3)$,如果决策不成环的话,我们可以用 dijkstra 来解决。
因为 dijkstra 有一个特性,就是每次出队的都是最小的元素,那么我们每次把已知的最小的期望 push 进堆里面,然后更新它能更新到的节点,类似于最短路,最后输出结果就行了,此处不再赘述。(详见后面的期望 DP)
4、最短路径树/有向无环图
对于每一条可能在以 $s$ 开头的最短路上的边(边权为正),全部拿出来就成了最短路径树,如果不保证最短路只有一条的话,那么这棵树会变成有向无环图。
在这个有向无环图上,我们可以统计每个点被经过的次数,每条边在所有路径中被经过的次数,甚至可以处理动态询问修改一条边后的从 $s$ 到 $t$ 的最短路。
所有用法都来自于它的几条性质:
每条边都出现在至少一条最短路中。
结果是树或有向无环图。
欧拉路径
这个知识点难就难在建模。
例1:对于一个 $n$ 个节点 $m$ 条边的无向图,找到最小的路径覆盖,使得每条边最多被覆盖 $1$ 次。(路径可以是环)
很显然,剖分成 $k$ 个欧拉路径就可以了。
如果图有 $k$ 个奇数度数的节点,答案为 $\frac{k}{2}$ (非整数则无解)条,否则如果图没有边答案为 $0$,有边答案为 $1$。
输出答案的方式也很巧妙,可以新建一个虚点,对于图中所有个连通块的奇数节点连边,若某个连通块的节点全是偶数节点,则选择一个连双向边就可以了。
最后由于整张图有一条欧拉通路,用 DFS 把欧拉通路求解出来,然后用新增的边把这些通路分成几段,段数就是答案,顺便还把方案求出来了。
例2:
有 $4 \times n$ 颗宝石,价值分别为 $1 \sim 4 \times n$。
宝石的颜色共有 $n$ 种,每种颜色恰好有 $4$ 颗宝石。
现在要将宝石装进两个箱子,满足以下两个条件:
- 两个箱子的宝石总价值相等。
- 每个箱子每种颜色恰有 $2$ 颗宝石。
请你设计一种划分方案,数据保证一定存在符合条件的划分方案。($1 \le n \le 2\times 10^5$)
考虑构造,对于每组 $i+j=4 \times n$ 的 $i,j$,将 $a_i$ 与 $a_j$ 连边,然后我们发现,每种颜色会连偶数条双向边($2$ 或 $4$),就必然存在一条欧拉路径,把欧拉路径跑出来之后,因为每条边都代表两个宝藏,所以我们从这些边中选不相交的边(奇偶分类即可),输出方案。
还有一道神仙题,不说解法:AT-agc017e Jigsaw。
其它
差分约束:方程列出来就很简单了。
拓扑排序:基础算法。
PART-2
有向图连通性
主要算法是 Tarjan,解决一些与连通(每个点的点权不能重复计算)相关的题目。
主要步骤,任何有向图缩点后均变为有向无环图,我们这时便可以在 DAG 上 DP 出最长链等经典问题。
因此,此处不介绍经典问题,均介绍变种。
例1:P1407 [国家集训队] 稳定婚姻。
很显然,像二分图一样,如果夫妻能够找到一个环,并且满足其余夫妻能够匹配成功。
所以边双的做法是错误的,我们要对于原夫妻关系从丈夫到妻子连边,其它情侣关系从女方向男方连边,判断也很简单,就判断原夫妻是否在一个强连通分量中即可。
例2:P2403 [SDOI2010] 所驼门王的宝藏。
因为只有 $n$ 个藏宝宫室,所以考虑对这 $n$ 个节点建立有向边。
对于可以走 $8$ 个方向的宫室,暴力连边即可,$O(n)$。
但是有些宫室可以走到一行/一列内任意宫室,我们这时可以用到最短路的技巧,对于每行/每列建虚点,点权为 $0$ 就可以了,然后向对应的节点连入边/出边即可。
最后 Tarjan 缩点后跑最长链。
例3:P4819 [中山市选] 杀人游戏。
很显然,对于入度为 $0$ 的 scc,知道了一个就可以知道以它为开头的所有 scc 的身份。
但是有一种特殊情况,就是会存在一个入度为 $0$ 的 scc 使得它的大小为 $1$ 并且其它入度为 $0$ 的 scc 选了之后只剩下它一个,我们就可以直接推断出它是什么身份。
这种情况也很好判断,只需要知道它的儿子节点有没有除了它之外其它的入边就行了。
总时间复杂度 $O(n)$。
例4:P4700 [CEOI2011] Traffic。
这道题有一个特殊限制,所有边在平面直角坐标系中都不相交,这样就有一个结论:
- 排除开不能被左边节点到达的右边节点,那么每个节点能到达的右边节点都是在某一个 $[x,y]$ 范围内的所有节点。
(以上节点均为 scc 缩点后有向无环图上的节点)
这个性质比较好证,画个图理解即可。
最后在有向图上 DP,暴力合并区间即可。
例5:P8328 [COCI2021-2022#5] Usmjeravanje。
根据 scc 的传递性,我们可以知道当两条不同航线构成一个 X 形状的时候,X 的上下两部分会互相连通。
再根据一个贪心原则,有 X 形状的一定让它构成,证明不在赘述。
最后确定每条边的方向后,用并查集维护或者直接跑一遍 Tarjan 就可以了。
例6:P7737 [NOI2021] 庆典。
还是缩点之后考虑图的形态,因为如果有 $x \to z,y \to z$,一定有 $z \to y$ 或 $y\to z$。
所以最后缩点之后的形态一定是一棵只有一个 $0$ 入度节点的叶向树。(从祖先连向儿子的边可以去掉,不影响连通)
然后对于 $k=0,1,2$ 的情况分类讨论,对于每个可能到达的 scc,它的祖先一定有一个可以被起点到达,它的后代一定有一个可以到达终点。
我们就剖分成了几条链,最后用虚树做一下链合并就可以了,用树剖的话时间会多一个 $\log$。
综上,有向图连通性是有向图的一个大板块,而且经常和 DP 一起使用,难的题做起来比较麻烦且极具挑战性。
无向图关于点的连通性
基本上和圆方树一起使用,可以 $O(n)$ 维护删掉每个点之后的连通块的一些信息。
例1:P5058 [ZJOI2004] 嗅探器。
从 $s$ 开始跑 Tarjan,然后对于每个在 $s$ 之下 $t$ 之上的割点,都有可能成为答案。
例2:P4494 [HAOI2018] 反色游戏。
首先对于每个连通块,如果它的 $1$ 的个数是偶数,那么答案为 $2^{m-n+1}$。
- 证明:首先找到任意生成树,一定有且仅有一种情况满足要求,然后剩下 $m-n+1$ 条边随意选择 $0,1$,都可以满足条件。
用圆方树维护删去每个节点的连通块的大小就可以了。
一些性质:
无向图关于边的连通性
更少了。
所有题目大概就是缩完点之后在树上跑一个 DP 就可以了,感兴趣的可以做一下 P8867 [NOIP2022] 建造军营。
以上就是第一部分图论学习笔记,下一部分预计:二分图,网络流,费用流等。

