Prüfer 序列

Prüfer 序列 (Prüfer code)，这是一种将带标号的树用一个唯一的整数序列表示的方法。

注意：我们不考虑含有 $1$ 个结点的树。

构建方式

找到一个编号最小的叶子节点，从树上删除，然后把它唯一指向的节点添加到一个序列 $a$ 中，直到树上只剩 $2$ 个节点。

堆的构造过程很简单，此处介绍线性构造过程：

首先找到当前最小的叶子，删去添加进序列后，如果他唯一指向的节点这时也变成了一个叶子且这个节点的编号小于当前编号，那就递归下去。

否则编号自增继续检查。

一共执行 $n-2$ 次，刚好删去了 $n-2$ 个叶子结点。

反构建

给出 Prüfer 序列，然后让你构造出一棵树满足这个序列。

堆的做法很简单，此处不讲。

那么我们肯定取出来不在这个序列里的最小的数，然后连向第一个点，然后把第一个点删掉，然后持续这个过程即可。

那么我们还是尝试指针的算法解决。

首先找到当前最小的节点，连边之后如果它连的那个边的端点也没有在后面的序列出现过且节点编号小于当前节点编号，那么递归下去。

否则编号自增继续检查。

一共执行 $n-2$ 次，最后一条边手动连即可，刚好 $n-1$ 条边。

性质

每个序列的元素都可以随便取，且一定能够构成一棵树，那么一张完全图的生成树个数就有 $n^{n-2}$ 种。

可以通过这个性质解决很多关于树的计数问题。

同余最短路

设 $f_{i}(0 \le i <x)$，表示状态，状态大多数定义为 $y \bmod x=i$ 下每个 $y$ 的某个附带参数的最小值。

那么我们可以根据类似于动态规划之间的相互转移来构建出一幅图，根据图的边权决定最短路的时候是用 $\texttt{SPFA}$ 还是 $\texttt{dijkstra}$。

用一道例题就可以解决这个知识点：

求一个 $y \bmod x = 0(y>0)$ 使得 $y$ 的各个位数之和（10 进制）最小。（$1 \le x \le 10^5$）

很明显，我们用 $f_i$ 表示模 $x$ 为 $i$ 的所有 $y$ 位数之和最小是多少。

那么每个 $i$ 都可以转移到 $(10i+k) \bmod x(0 \le k \le 9)$，然后边权是 $k$。

最后跑最短路就可以了，答案是 $f_0$，初值需要注意一下，不能把 $0$ 弄进去，所以最开始 $\texttt{push}$ 进 $1 \sim 9$ 即可，需要 $\bmod \ x$。

大概这种思想就是同余最短路，旨在去掉相同和无用的状态，促进题目的解决。

Kruskal 重构树

主要是把从 $x$ 到 $y$ 路径上最大值的最小值或者最小值的最大值转化为点权，最后构成一棵 $2n-1$ 个节点的树。

在执行 kruskal 的过程中，如果需要连接 $x$ 和 $y$ 的边，然后新建一个节点 $p$，$p$ 的权值为这条边的权值，然后 $ls_p \gets x,rs_p \gets y$。

我们最后发现这样子构建出来的树也是一棵二叉树，然后就可以执行最大值的最小值或者最小值的最大值的一些 dp 问题。

或者是一棵树上的边权最小值或者最大值之类的题目。

无向图耳分解

定义无向图的一个”耳”为其任意一条简单路径或者一个简单环，例如下图红色边和黄色边连接形成的就是无向图的一些耳的形态：

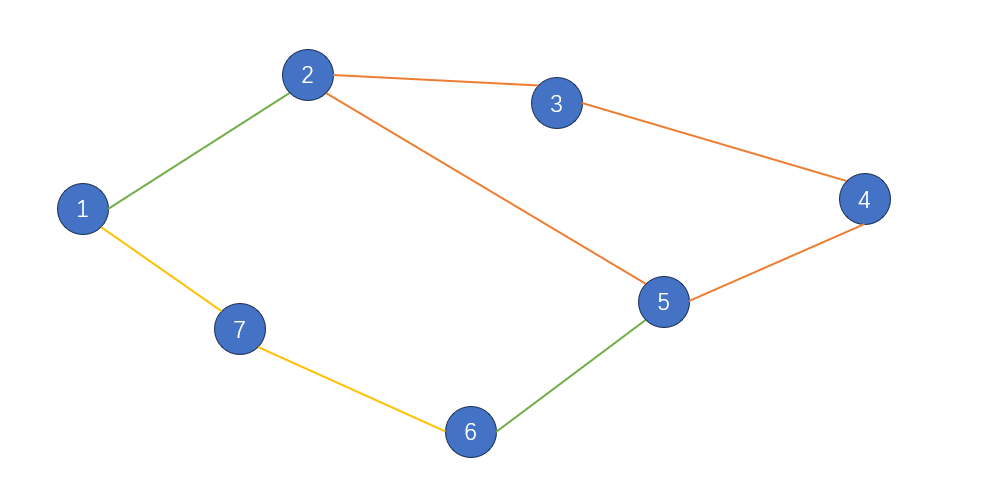
其中简单路径称为开耳，即上图中的黄色部分。

称一个“耳”可删除，当且仅当如果这个耳是开耳，删掉除端点外的所有点及其相连的边之后这个图仍然连通；如果不是开耳，那么保留这个简单环的一个端点，删掉除这个端点外的所有点及其相连的边之后这个图仍然连通。

例如上图中，$6-5-2-3$ 就不可以被删除，因为删除之后 $4$ 号节点会单出来；$2-3-4-5$ 可以删除，但是必须保留 $2$ 或者 $5$ 号节点，否则不连通。

如果这个图可以一直删除耳直到只剩一个节点，那么称这个过程是“耳分解”，如果除了最后一次剩下的删除的耳都是开耳，那么这个过程就是“开耳分解”。

最后，图是边双连通图和这个图具有“耳分解”等价，因为割边不可能出现在任何一个可删除的耳中，并且边双连通图可以按照下面的方式构造耳分解。

也就是用 Tarjan 得到若干返祖边，然后这些返祖边按照上端点的深度排序之后按照下图方式构建耳分解即可，但是分解的时候需要把顺序倒过来，并且可以证明每次加入的都是一个耳：

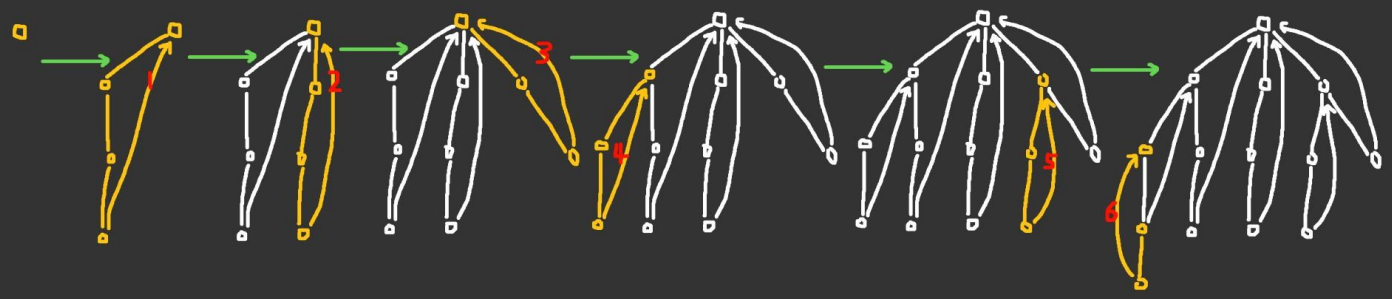
还有，图是点双连通图和这个图具有“开耳分解”等价，这个可以通过上述证明得到，即所有耳一定都是形如 $6$ 号耳的形态，不会形成一个环。

双极定向

给定一个无向图和 $s,t$ 试给每条边定向，满足这是一个有向无环图，并且 $s$ 可以到达所有点，$t$ 可以被所有点到达。

如果添加一条 $s-t$ 的边，那么这个无向图如果存在定向方法，它一定是一个点双连通分量，证明根据定义，删掉任何一个点之后无向图都是连通的。

如果它添加之后是点双连通，那么我们接下来考虑构造一种定向方法：

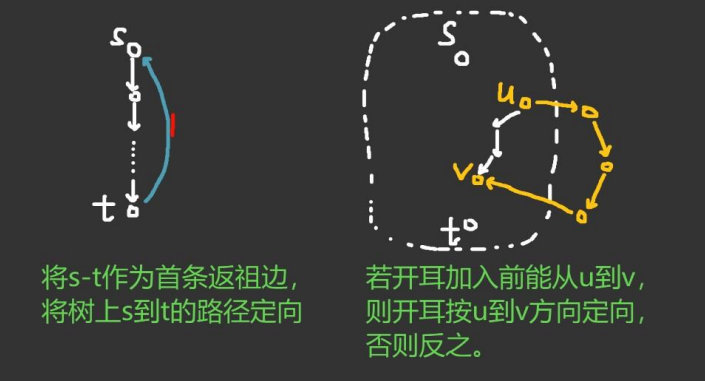
首先以 $s$ 为根，加入 $s-t$ 边，然后用 Tarjan 得到一棵 DFS 树，之后我们可以直接让 $s \to t$ 路径上的所有边往下定向，并且 $s-t$ 边也往下定向，接下来我们考虑对这幅图进行一个耳分解。（当然要去掉 $s-t$ 这一条返祖边）

首先把所有返祖边按照最浅的那个点的深度排序，然后设当前加入的返祖边为 $u \to v$，我们考虑 DFS 树上 $u$ 到 $v$ 这一条路径，因为按照了深度排序，所以从 $u$ 往下的那一条边一定是定向了的，如果这条边是父亲向儿子，那么这个耳就定向为 $u \to v$，并且从 $v$ 开始在 DFS 树上跳父亲，每次经过一条没有被定向的树边都定向为儿子向父亲，直到有一条被定向了的树边，那么直接 break 即可，因为这条边上方的所有边一定都被定向了。

如果 $u$ 往下的那条边是儿子到父亲，那么这个耳被定向为 $v \to u$，并且依然跳父亲，不过所有树边都定向为父亲向儿子。

总的来说，时间复杂度是 $O(n)$ 的，如果用倍增找 $u$ 往下的那条边就是一个 $\log$，构建过程如下图所示：

代码如下，细节比较多：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84

#include<bits/stdc++.h>
#pragma GCC optimize("Ofast")
#define ll int
#define N 600005
using namespace std;
struct node{ll x,y,id;}p[N];
vector<pair<ll,ll> > op[N];
ll n,m,i,temp,dcc,dfn[N],low[N],tot,sta[N],top,dep[N],ttt,x[N],y[N],fath[N],vis[N],st[N][21],tofa[N],ans[N];
inline bool cmp(node a,node b){
	if(dep[a.x]==dep[b.x]) return a.y<b.y;
	return dep[a.x]<dep[b.x];
}
inline void tarjan(ll x,ll fa){
	for(ll i=1;i<=20;i++) st[x][i]=st[st[x][i-1]][i-1];
	dfn[x] = low[x] = ++tot,sta[++top] = x;
	for(ll i=0;i<op[x].size();i++){
		if(!dfn[op[x][i].first]){
			st[op[x][i].first][0] = x,dep[op[x][i].first] = dep[x]+1,fath[op[x][i].first] = x,tarjan(op[x][i].first,x);
			low[x] = min(low[x],low[op[x][i].first]);
			if(low[op[x][i].first]>=dfn[x]){
				dcc++;
				while(sta[top+1]!=op[x][i].first) sta[top--];
			}
		} 
		else if(fa!=op[x][i].first){
			low[x] = min(low[x],dfn[op[x][i].first]);
			p[++ttt] = (node){op[x][i].first,x,op[x][i].second};
			if(dep[p[ttt].x]>dep[p[ttt].y]) swap(p[ttt].x,p[ttt].y);
		}
	}
}
inline void solve(ll x,ll y,ll &z){
	top = 0;
//	cout<<"! "<<x<<" "<<y<<endl;
	for(ll i=y;i;i=fath[i]){
		if(vis[i]) break;
		vis[i]=1,sta[++top]=i;
	}
	ll depth = dep[y]-dep[x]-1,pos = y;
	for(ll i=20;i>=0;i--) if((depth>>i)&1) pos = st[pos][i];
	ll temp = tofa[pos];
	if(temp==1){
		z=1;
		for(ll i=1;i<=top;i++) tofa[sta[i]]=0;
	}
	else{
		z=0;
		for(ll i=1;i<=top;i++) tofa[sta[i]]=1;
	}
}
int main(){
	ios::sync_with_stdio(false);
	cin>>n>>m;
	for(i=1;i<=m;i++){
		cin>>x[i]>>y[i];
		if(!((x[i]==1&&y[i]==n)||(x[i]==n&&y[i]==1))){
			op[x[i]].push_back(make_pair(y[i],i));
			op[y[i]].push_back(make_pair(x[i],i));
		}
	}
	op[1].push_back(make_pair(n,0)),op[n].push_back(make_pair(1,0)),dep[1]=1,tarjan(1,0);
	if(dcc!=1){
		cout<<"-1\n";
		return 0;
	}
	sort(p+1,p+ttt+1,cmp);
	for(i=n;i;i=fath[i]) tofa[i]=1,vis[i]=1;
	for(i=1;i<=ttt;i++){
		if(p[i].x==1&&p[i].y==n) continue;
		if(p[i].x==p[i-1].x&&p[i].y==p[i-1].y) continue;
		solve(p[i].x,p[i].y,ans[p[i].id]);
		if(x[p[i].id]==p[i].x) ans[p[i].id]^=1;
	} 
	for(i=1;i<=m;i++){
		if(x[i]==1&&y[i]==n) cout<<0<<endl;
		else if(x[i]==n&&y[i]==1) cout<<1<<endl;
		else{
			if(fath[y[i]]==x[i]) cout<<(!tofa[y[i]])<<endl;
			else if(fath[x[i]]==y[i]) cout<<tofa[x[i]]<<endl;
			else cout<<ans[i]<<endl;
		}
	}
	return 0;
}

证明

采用数学归纳法，设每次确定的树边的连通块为 $S$，并且 $S$ 中的每个元素都可以被 $s$ 所到达，并且都可以到达 $t$，容易发现一开始的 $s \to t$ 路径定向是满足这个条件的，每次加入一个耳，即简单路径，这个路径的定向也是满足这个条件的，因此，算法得证。