插入类型 dp
插入类型 DP
形式
多为 $n$ 个元素无法重复使用,需要给定一个排列,满足一定条件或是求有多少个排列满足一定条件。
$n$ 一般在 $100 \sim 5 \times 10^3$ 左右。
满足一些函数图像,类似于波浪函数,且答案与每个波浪和波浪的顶点有关(函数的 $x$ 坐标为下标,$y$ 坐标为下标上数的值)。
满足以上三个条件的 DP 大部分是插入类型的 DP。
引入
先来看一道例题:
- 对于一个正整数序列 $a$,长度为 $n(n \ge 3)$,如果对于所有的 $2 \le i \le n-1$,都有 $a_{i-1}+a_{i+1}\ge 2a_i$,就称这个序列是“美丽的”。现在给你另一个正整数序列 $b$,问你有多少种排列这个序列的方式使得这个序列是美丽的。($n \le 100$)
这道例题看似无从下手,但是我们把式子变换一下可以发现:
$$
a_{i-1}+a_{i+1} \ge 2a_i \to a_{i-1}-a_i \ge a_i-a_{i+1}
$$
即差分递增,差分递增有什么好处呢?把所有满足条件的 $a$ 序列列举出来,就会发现它其实是先是一段递减,然后中间可能会有平的一段(差分为 $0$),最后一段递增。事实上就是一个有平台的单谷函数。
有了这个性质,我们按 $a$ 从小到大排序,然后依次插入进这个函数,每个数可以插入到函数的左边,或者右边。(因为已经排好序了)
于是设 $dp_{i,j,k,l}$ 表示左边为 $i,j$ 且 右边为 $k,l$ 的方案数总和。
注意观察:这个 DP 没有后效性,且能够顺利转移,满足子问题包含的性质。
综上,可以 $O(n^4)$ 解决。
实践
容易看出,引子是一个水题,因为我们还没有牵扯到其它的限制,只是规定元素不能重复选,接下来我们看一下这道题:
这道题就满足了上面三条形式:
$n$ 个元素无法重复使用,求有多少个排序满足一定条件。
$2 \le n \le 2\times 10^3$
波浪函数,每个波浪的长度为 $1$
这个时候,考虑怎么转换已经没有用了,因为它并不满足类似于差分递增这种规律,使得有一个单调性在里面,所以我们按照这三条形式的最后一条,即波浪进行入手。
先看下面一幅图:
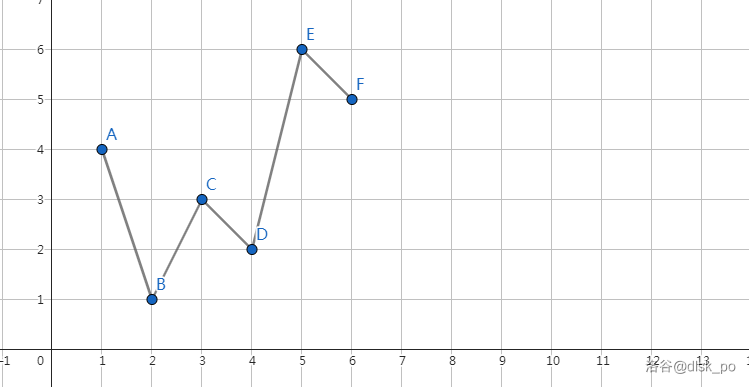
(如图,这是$n=6,s=4,t=5$ 时候的一种情况。其中 $y$ 轴代表点的编号,$x$ 轴代表访问的顺序,即从 $1$ 访问到 $n$)
那么我们观察到这个函数图像有 $5$ 段(因为每段必须长度为 $1$)。段长不好设计 DP,那我们考虑用段的个数来设计 DP。
这种类型的 DP,有几个要素:
- 确定元素添加顺序
- 确定状态的转移
- 确定对于 $s,t$ 的特判
我们一个问题一个问题解决。
确定元素添加顺序
没什么好说的,既然是排列,那就要从 $1\sim n$ 挨个添加。
确定状态转移
因为必须在 $O(n^2)$ 时间内通过此题,所以设 $dp_{i,j}$ 表示从 $1 \sim i$ 中,分成了 $j$ 段的方案数,容易得知,最后的答案是 $dp_{n,1}$。
什么叫段数,请看这幅图:
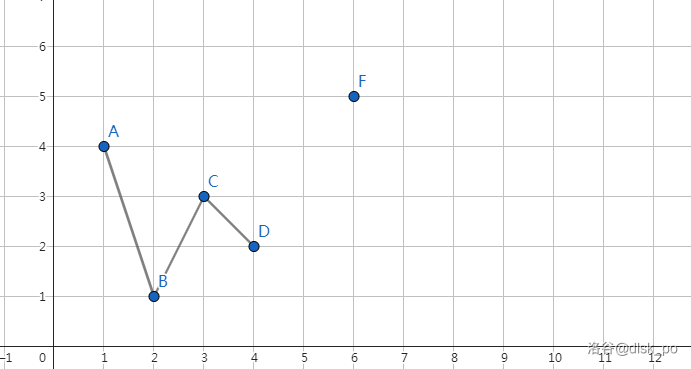
这里,就是把 $1 \sim 5$ 分成了两段:$A \sim D,F \sim F$。
因为我们的 $s$ 需要特判,所以把它归在 $B \sim D$ 这个段里,准确的说,每个段应该是类似于 $M$ 形的(可以有很多拐弯,但是第一个是上升,最后一个下降)。为了准确计算,$s$ 和 $t$ 都并到相邻的段里面。
考虑转移,因为我们选择了 $1\sim n$ 这种顺序,那么我们每个 $i$ 都是在选了比它更小的数之后决策,再加上每个段是 $M$ 形状,所以 $i$ 可以把两个段合并成一个,或者自己新开一个段。
综上,DP 方程就可以出来了:
$$dp_{i,j} = \begin{cases} dp_{i-1,j}+dp_{i-1,j-1} & i=s \text{ or } i=t\ jdp_{i-1,j+1}+(j-[i>s]-[i>t])dp_{i-1,j-1} & \text{other wise} \end{cases}$$
总述一下,这种类型的题其实大部分都是对段进行 DP,然后考虑转移和特判,之后就可以过了。
小结
此类 DP 被称为 “插入DP” 或者是 “连续段DP”,主要都是依据段数来转移状态。
模型:$1 \sim n$ 的元素不能重复使用,按照某个顺序排列 $i,j$ 能够使得 $i,j$ 的贡献成为定值。
不同之处:有些题目固定了左右两端点,有些题目没有固定左右两端点。
依据题目的不同要求,大部分题目中的段是可以 $A,W,V,M$ 等形状的,但少部分题目(例题)则限制了形状,但归根结底转移都是一样的套路。
设计转移时通常 按照一定顺序插入,且知道了这个顺序就知道了题目中要求的函数的值(函数的值是根据数的一定顺序决定的) 且 每个元素只有合并两段、接续一段、新开一段等操作,这样才能更好的帮助我们维护 DP 数组。(有些时候元素插入在一段的左/右边的结果不一样,需要再开一维)
推这种 DP 式子的时候,我们会发现有些情况可能会缠在一起,让人分不清楚。这里要着重说一下:每个状态其实都是在为后面的状态作准备。
比如:
明明可以写为接在一个段的后面,DP 方程中偏要写为新开一个段。这就是因为新开一个段能够保证这个元素的左右两边都是比它大的数,如果是接续一个段,那么只能保证一端比它大,一端比它小。
所以,我们对于新开一个段和接续一个段的状态会不会重复的问题,只需要考虑它们最后形成的状态会不会重复就行了,而并不需要考虑当前的形态相不相同。例如:$1,3,2,4$ 中如果 $4$ 是接续的 $2$ 后面,那最后就有可能是 $1,3,2,4,\cdots$,即 $2,4$ 中间不会有任何元素;如果 $4$ 是新开了一个段,那么最后就可能是 $1,3,2,\cdots,4,\cdots$。那有些人就会有问题:如果 $2$ 后面的省略号的内容为空的话,那不就相同了吗?不会,因为这样的话,因为 $4,2$ 不在一个段,所以这里至少有两段,而我们最终统计答案的时候是只统计 $1$ 段的,意思是中间至少有一个元素把这两段合并起来,就与最开始的假设矛盾了,故状态不会重复。
最后,特别要注意整个序列两个端点需要特别判断,处理这种类型的方法有两种:
- 在转移过程中就把贡献去掉/加上。(多为题目固定了左右两端点)
- 多开两维数组记录两个端点的贡献或一些信息。(多为题目没有固定左右两端点)
习题
- CEOI2016-kangaroo(例题)
- AT_abc209_f-Deforestation
- AT_dp_t-permutation
- [COCI2021-2022#2] Magneti
- CF1515E-Phoenix and Computers
- CF704B-Ant Man
- [JOI Open 2016] 摩天大楼
- [ZJOI2012]波浪
部分习题讲评
CF704B-Ant Man
初探题面
这道题我们可以先转换一下题意:
让 $a_i \gets a-i+x_i,b_i \gets b_i-x_i,c_i \gets c_i+x_i,d_i \gets d_i-x_i$。
那么就可以将 $f(i,j)$ 写为:
$$
f(i,j) = \begin{cases} d_i+a_j & i<j\ c_i+b_j & i>j \end{cases}
$$
由这个公式看出:权值与下标的大小相关,只要确定了下标的大小,那么这个权值基本上就确定了。
所以,按照 $1\sim n$ 的顺序插入 DP。
状态设计
还是像例题一样,设 $dp_{i,j}$ 为 $1 \sim i$ 中分成 $j$ 段最小的代价是多少。
但是与例题不同的是,这里的每一段可以是 $V,M,W,A$ 形状的,就是起始位置没有硬性要求。(对于起始位置的要求视题意而设计状态)
那么我们就可以开始 dp 了。
首先考虑一般情况($i \ne s \text{ and } i\ne t$):
(以下状态设计均考虑费用提前计算技巧)
- $i$ 能够把之前的两段拼起来,那么 $i$ 对于全局权值的贡献就是 $a_i+c_i$。
- $i$ 能够在一段的末尾与那一段拼起来,那么 $i$ 对于全局权值的贡献是 $a_i+d_i$。
- $i$ 能够在一段的前面与那一段拼起来,那么 $i$ 对于全局权值的贡献是 $b_i+c_i$。
- $i$ 独立成为一段,则贡献是 $b_i+d_i$。
所以对于 $i \ne s \text{ and } i \ne t$,转移有四种:
$$
dp_{i,j} = \min\begin{cases} dp_{i-1,j+1} +a_i+c_i \ dp_{i-1,j}+a_i+d_i \ dp_{i-1,j} + b_i+c_i \ dp_{i-1,j-1}+b_i+d_i \end{cases}
$$
注意,这些式子是怎么推导出来的!
- 因为贡献只与两个数的大小有关
- 两个数的大小这么来判断:比 $i$ 先填的数一定比 $i$ 小,比 $i$ 后填的数一定比 $i$ 大。
根据这两点,权值和方程就能很轻松写出来了。
至于 $i=s \text{ or } i=t$ 的情况,一个是只能加在某一段的后面,一个是只能加在某一段的前面,两个都可以自己成为一段,等待后面的元素把两段拼在一起!
细节
1、对于以 $s$ 开头的一段,不允许有任何元素拼在前面;对于以 $t$ 结尾的一段,不允许有任何元素拼在后面。
2、对于以 $s$ 开头的一段和以 $t$ 开头的一段,一定到最后才能拼起来,不能在前面就合成了一个段。
3、为什么我们合并两个段不需要额外记录是不是 $s$ 和 $t$ 所在的段?因为不管是合并哪两个段事实上是一样的,只要有一个段没有 $s$ 和 $t$,那么这个合并就可以进行。
4、为什么考虑加在某个段的前面的时候不需要判断 $s$,$t$ 也不需要判断?因为我们加到任意一段前面/后面的代价是一样的。(都是费用提前计算)
5、做这类题目时,一定要把 $i$ 和 $j$ 的关系分开(常用方法:费用提前计算),不然无法记录状态!
综上,这道题目就做完了,为了避免一些特殊情况,代码采用从前往后的方式 DP。(从后往前也可以)
1 |
|
[JOI Open 2016] 摩天大楼
初探题面
首先,看到绝对值想到分类讨论,即为:
$$
g(i,i+1) = \begin{cases} f_i-f_{i+1} & f_i \ge f_{i+1} \ f_{i+1}-f_i & f_i < f_{i+1} \end{cases}
$$
那么又是根据大小关系来决定权值大小了,所以考虑插入 DP。
第一种方法
状态推导
像上一道题一样,这里的状态因为没有段长的硬性要求,所以 $W,V,A,M$ 形状的段都是可以的,因此也减少了初始和结尾字符的特判(尽管题目也不需要特判)。
设 $dp_{i,j,k}$ 表示 $1\sim i$ 这些数所代表的数值插入进去之后有 $j$ 段当前权值总和为 $k$ 的情况总数。
注意到最开始是不用 $f_1-f_0$ 或者 $f_0-f_1$,结尾同理,所以依旧需要特判。
再发现,如果我们不记录开始和结尾数值的话,很难维护,所以我们要 用尽可能小的空间传递更多的信息。
- 如果我们能够确定第一个位置是否已经被填了,那么就不存在其它特判情况了,即在填的时候特判一下就可以了。(结尾同理)
根据上面那一条发现的性质,我们对 DP 状态进行修改,设 $dp_{i,j,k,0/1,0/1}$ 表示 $1\sim i$ 这些数所代表的数值插入进去之后有 $j$ 段当前权值总和为 $k$ 且开头结尾有没有被确定的情况总数。
这个转移方程一确定,那么事情就简单多了。
转移方程
首先,明确一下状态的后效性如何去除(因为 $g(i,i+1)$ 与两个元素有关)。
看下面这幅图: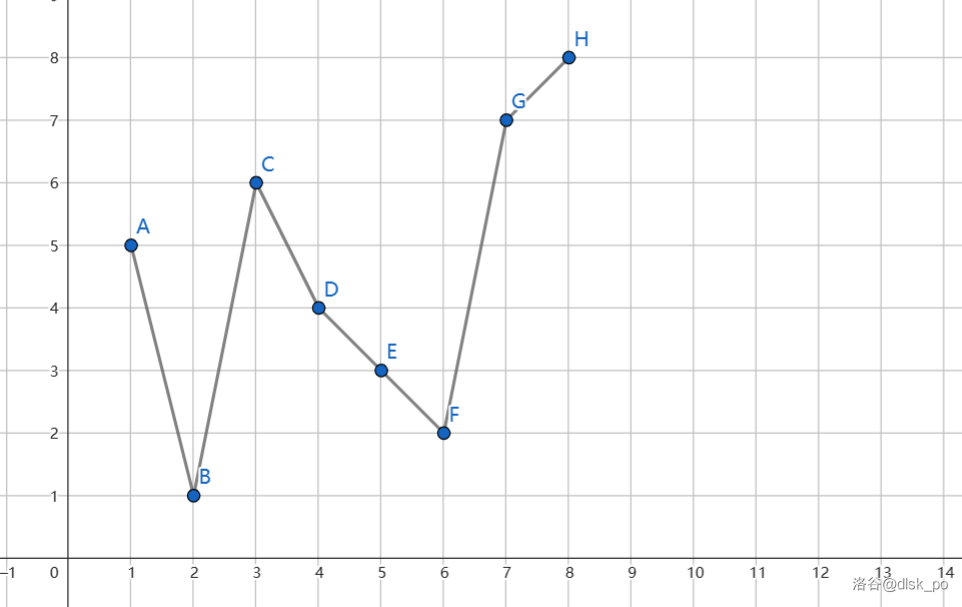
(其中横轴为元素的位置,纵轴为元素的值)
容易看出这样的总的权值和是:$|5-1|+|1-6|+|6-4|+|4-3|+|3-2|+|2-7|+|7-8|$ 的。
在我们按照大小顺序插入的前提下考虑分开:$5-1+6-1+6-4+4-3+3-2+7-2+8-7$,消项得:$5-1+6-1+6-2+8-2$。
这样我们就可以得知,每个极小值会被减去两次(但是如果是在序列开头或末尾只会被减一次),每个极大值会被加两次(但是如果是在序列开头或末尾只会被加一次)。
即遇到极大值看它是不是在开头或者末尾,如果在,贡献就会一份,否则为两份,极小值同理。
综上,我们就把 $i,i+1$ 的贡献分开了,而且也利用到了我们知晓元素之间大小关系的性质,DP 转移就可以开始执行了。
以下状态设计均为从大往小插入考虑
然后,熟悉的分类讨论:
- 对于 $i$,它合并了两个段,段数少 $1$
因为 $i$ 合并两个段,所以它不能在最左边或者最右边,而且它两端都是比它小的数,那么它便是这个区间的极小值,对全局的贡献是负的两倍。即:
$$
dp_{i,j,k,p,l} = jdp_{i-1,j+1,k+2a_i,p,l}
$$
(为什么是加 $2a_i$,是因为,它插入之后贡献为 $k$,插入之前肯定就是加上)
- 对于 $i$,它新开了一个段,段数多 $1$
因为 $i$ 新开了一个段,之后合并它和其它段的数一定比它小,所以它是区间极大值,对全局的贡献是正两倍,注意,它如果是在最左边,它的贡献就只有一倍,在最右边同理。特别注意,如果左右两边已经确定了,那么它能够新开段的位置会少 $1\sim 2$ 个。即:
$$
\begin{aligned}
dp_{i,j,k,0,0} &= jdp_{i-1,j-1,k-2a_i,0,0} \
dp_{i,j,k,0,1} &= (j-1)dp_{i-1,j-1,k-2a_i,0,1}+dp_{i-1,j-1,k-a_i,0,0} \
dp_{i,j,k,1,0} &= (j-1)dp_{i-1,j-1,k-2a_i,1,0}+dp_{i-1,j-1,k-a_i,0,0} \
dp_{i,j,k,1,1} &= (j-2)dp_{i-1,j-1,k-2a_i,1,1}+dp_{i-1,j-1,k-a_i,1,0}+dp_{i-1,j-1,k-a_i,0,1}
\end{aligned}
$$
- 对于 $i$,它延续了某个段,并接在该段的左/右边,段数不变
我们以左边为例,因为 $i$ 在普通情况下一边会有比它小的,一边会有比它大的,所以 $i$ 对总的值没有贡献,但是当 $i$ 在左边或者右边时,它是区间极小值,贡献是负一倍。即:
$$
\begin{aligned}
dp_{i,j,k,0,0} &= jdp_{i-1,j,k,0,0} \
dp_{i,j,k,0,1} &= jdp_{i-1,j,k,0,1} \
dp_{i,j,k,1,0} &= (j-1)dp_{i-1,j,k,1,0}+dp_{i-1,j,k+a_i,0,0} \
dp_{i,j,k,1,1} &= (j-1)dp_{i-1,j,k,1,1}+dp_{i-1,j,k+a_i,0,1}
\end{aligned}
$$
加在右边同理,由此我们推导完了整个 DP,但是实现过程中还要注意一下转移时的细节:左右端点固定后权值是多少?有多少个段可以插入等。
这种方法常数很大,同时不利于优化,但是个人认为思维跟 kangaroo 差不多,而且更好想一些。
第二种方法
此处不再赘述,详见:Afewsuns 的博客-[JOI Open 2016]摩天大楼题解。
注:[ZJOI2012] 波浪 和此题十分相像,主要是处理精度问题和小数的“快速输出”,那道题可能会卡常,推荐使用第二种方法。
此处给出第一种方法的代码:
1 |
|
[ABC209F] Deforestation
初探题面
这道题有点类似于前面提到的“凸”这道例题,但是它没有叫你计算最小的花费是多少,而是计算有多少种方案能够达到最小的花费。
遇到这种类型的题目,首先要明确在什么条件下能够达到最小的花费。
因为任意一个 $i$ 产生的权值与 $i-1,i,i+1$ 有关,说人话就是相邻的元素选择的顺序会影响到它的权值,所以我们考虑对于 $i,i+1$,哪个先选比较好。
- 如果先选 $i$,权值为:$a_{i-1}+a_i+a_{i+1}+a_{i+1}+a_{i+2}$。
- 如果先选 $i+1$,权值为:$a_i+a_{i+1}+a_{i+2}+a_i+a_{i-1}$。
用第一个式子减去第二个式子得:$2a_{i+1}-2a_i$。
所以当 $a_{i+1} > a_i$ 时,先选 $i+1$ 更好;当 $a_i > a_{i+1}$ 时,先选 $i$ 更好;如果两者相等,那么我们可以任意抉择。
很明显的,对于每组 $i,i+1$ 我们都可以这么抉择并且至少有一种方案满足这种选择,所以这种局部最优性可以扩展到全局,因此,我们只要求出满足这种顺序的方案数就行了。
状态设计
我们发现如果按照这个关系减出来的图其实是一个 TAG,不好维护插入顺序。因此我们只能考虑从 $1 \sim n$ 考虑插入。
因为 $i$ 可以插入的方案数仅与 $i-1$ 所插入的位置有关系,而且题目允许 $O(n^2)$ 的空间和时间,因此我们设计两维 DP 数组:$dp_{i,j}$ 表示第 $i$ 个数插入到了第 $j$ 个位置满足条件的方案。
说明一下,这里的第 $j$ 个位置并不是最终操作序列上的位置,而是操作序列只保留 $1\sim i$ 的子序列的相对位置。
对于 $a_i > a_{i-1}$ 先选 $i$,所以 $i$ 的相对位置一定在 $i-1$ 的相对位置的前面,故 $dp_{i,j} = \sum_{k=j}^i dp_{i-1,k}$。
对于 $a_i < a_{i-1}$ 先选 $i-1$,所以 $i$ 的相对位置一定在 $i-1$ 的相对位置的后面,故 $dp_{i,j} = \sum_{k=1}^{j-1} dp_{i-1,k}$。
对于 $a_i = a_{i-1}$ 都可以先选,所以全部情况都可以转移,故 $dp_{i,j} = \sum_{k=1}^{j-1} dp_{i-1,k}$。
注:
- 第一个转移方程从 $j$ 开始循环到 $i$ 是因为如果 $i-1$ 在 $1 \sim i-1$ 的第 $j$ 个位置,那么 $i$ 就可以插入到第 $j$ 个位置的前面使得 $i$ 在 $i-1$ 的前面并且相对位置也是 $j$。
- 第二个转移方程循环到 $j-1$ 的道理同上。
- 这种方法为什么能不重不漏,是因为两个不同的最终操作序列一定有一个 $i$ 在 $1\sim i$ 中的相对位置不同;两个相同的最终操作序列一定满足每一个 $i$ 在 $1\sim i$ 中的相对位置相同。
- 初始化 DP 的时候需要注意 $1$ 在 $1\sim 1$ 中的相对位置只有 $1$ 这一个。
综上,代码就可以写出来了。
1 |
|
CF1515E-Phoenix and Computers
初探题面
一看就知道是插入 DP,但是如何设计状态令人十分难为。
还是想用 $dp_{i,j}$ 表示开了 $i$ 台,构成了 $j$ 个连续段。
根据上面的总结,我们知道,只要这个状态所产生的的最终的所有的状态不会与另外一个不同的状态(同一阶段)所产生的不同的所有的状态相重合,那么这种做法就会做到不重不漏。
而且题目要求如果 $i-1$,$i+1$ 两台电脑都有开启的话,$i$ 号电脑也自动开启,这就说明题目限制了如果两个段的之间的长度 $\le 1$ 的话,就会自动合并成一段,这便启发了我们状态的设计:相邻两个段之间的长度为 $\ge 2$ 的未知数。
注意:这里的未知数指的是中间一定有超过一个电脑,相当于中间有 $2$ 个电脑和中间有 $3$ 个电脑的状态是等价的。
考虑这种方法会不会导致状态有重叠,答案是不会。
因为考虑最终的操作序列,肯定最后合并成了一段,合并成了一段就不存在某两段之间至少有 $2$ 台电脑这个说法了,并且因为中间有 $2$ 个电脑和中间有 $3$ 个电脑的状态是等价的,故考虑转移的时候也不会重复。
既然都推到这里了,那么 DP 方程就出来了。
首先,单独形成一段,$dp_{i,j}=j \times dp_{i-1,j-1}$。
然后加在某段的两边(这里的左右边是一样的,故不分开讨论):$dp_{i,j} = j \times 2 \times dp_{i-1,j}$。
最后连接连段,如果两段中间的未知数等于 $2$,那可以开 $2$ 台中的任意一台;如果未知数等于 $3$,那只能开中间那台;如果未知数是 $4$ 或更多,开的电脑就不止一台,并且都是上述 $2$ 种情况的延伸。$dp_{i,j}=j \times dp_{i-3,j+1}+j \times 2 \times dp_{i-2,j+1}$。注意这里 $i$ 为什么要 $-2$ 或者 $-3$,因为它会自动开启 $2,3$ 台电脑。
最后注意一下,这次枚举的顺序就是开机的顺序了,并不是电脑编号的顺序,因为题目的自动与手动是按照开机的顺序以及位置决定的,与电脑编号没有关系。
1 |
|
总结
总结其实都写在例题和习题讲评里面了,复制粘贴一遍其实没有用,重要的是去理解,并且收获自己的感受,这样才能让做题的思路更加敏捷精确。这就是插入 DP,一个非常巧妙但是很难理解的 DP 类型。