AC 自动机

AC 自动机

一月 14, 2024

AC 自动机

自动机

自动机的概念：自动机是一个有向图，它接收字符（信号）序列，并对其进行处理（识别和判定），以确定其能到达的最终状态和路径。图中的点对应字符，存在一个起始状态点，多个结束状态点。如果图中任意一个点，连出去的对应某字符 ch 的边最多只有一条，则称该自动机是确定性的（DFA）。如果图中任意一个点，连出去的对应某字符 ch 的边可能有多条，甚至存在不对应任何字符的边，则称该自动机是非确定的（NFA）。

构建

首先像 trie 树一样插入字符串，树上的每个节点代表的是根节点到这个节点经过的边上的字符所构成的字符串。

这些边称为“树边”，每个节点还有 fail 指针，这个指针指向了一个节点，这个节点代表的字符串是当前节点代表字符串的后缀，也是最长后缀。

这里引用一下 OI-wiki 的 AC 自动机部分的图：

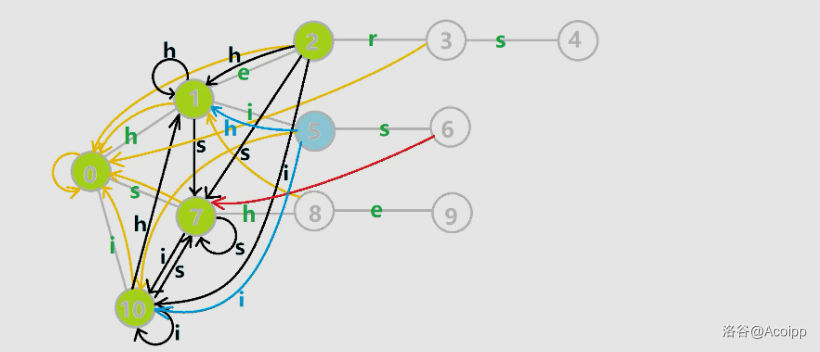
其中灰色的边就是字典树上的边，黄色的边就是 fail 指针，我们观察发现 $8$ 号节点代表的字符串是 $\texttt{sh}$，它的 fail 指针就是 $1$ 号节点，因为 $1$ 号节点代表的字符串是 $\texttt{h}$，是它的最长后缀。

但是 $3$ 号节点的 fail 指向根节点，代表没有任何一个字典树上的节点代表的字符串是它代表字符串的后缀。

接下来是构建函数 build：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void build() {
  for (int i = 0; i < 26; i++)
    if (tr[0][i]) q.push(tr[0][i]);
  while (q.size()) {
    int u = q.front();
    q.pop();
    for (int i = 0; i < 26; i++) {
      if (tr[u][i])
        fail[tr[u][i]] = tr[fail[u]][i], q.push(tr[u][i]);   //直接指向 fail[u] 的第 i 个儿子
      else
        tr[u][i] = tr[fail[u]][i];
    }
  }
}

查找

这是一个用于多模式串匹配的数据结构，例如我们要查找一堆串在 $T$ 中出现了多少次怎么办呢？

首先得记录第 $i$ 个节点所代表的字符串出现了那一堆串中间的串，在构建 trie 树的时候要加上一句 cnt[p]++，并且构建 AC 自动机的时候要在 q.pop() 后面加上 cnt[u] += cnt[fail[u]] 才行。

因为 $fail_u$ 有的字符串 $u$ 一定也有，并且不会计算重复，因为 $fail_u$ 是 $u$ 的最长后缀。

最后查询的时候把 $T$ 放进 AC 自动机里面走边就可以了，还要开一个变量存储次数。

1
2
3
4
5
6
7
8
int query(char *t) {
  int u = 0, res = 0;
  for (int i = 1; t[i]; i++) {
    u = tr[u][t[i] - 'a'];  // 转移
    res += cnt[u];          // 记录
  }
  return res;
}

如果我们想要查找每个字符串分别出现了多少次怎么办呢？容易发现 fail 树实际上就是一个后缀跳到后缀的过程，如果 $T$ 在上面的函数中经过了 $h$ 节点，那么 $T$ 一定包含了 $h$ 的所有祖先节点所代表的字符串，如果将它们的 $cnt$ 值都加上 $1$，答案也不会影响，于是我们可以记录经过的点，然后用拓扑排序在 fail 树上跑就可以了。

这里是 P5357 【模板】AC 自动机 的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include<bits/stdc++.h>
#define N 2000005
using namespace std;
//AC自动机中，fail数组最重要，代表了最长后缀的失配数组
int n,i,trie[N][27],tot,vis[N],fail[N],ans,cnt[N],res,id[N],j,in[N];
string temp,s[200005];
deque<int> op;
map<string,int> opp;
//add函数就是普通trie中的add函数
inline void add(string temp,int id){
	int p = 0;     //节点号
	for(int i=0;i<temp.size();i++){
		if(!trie[p][temp[i]-'a'+1]) trie[p][temp[i]-'a'+1]=++tot;
		p = trie[p][temp[i]-'a'+1];
	}
	vis[p]=id;     //标记一下
}
inline void build(){         //开始建造AC自动机
	for(int i=1;i<=26;i++) if(trie[0][i]) op.push_back(trie[0][i]);      //首先把根节点的儿子push进去
	while(op.size()){
		int tmp = op.front();
		op.pop_front();
		for(int i=1;i<=26;i++){       //for循环字符集
			if(trie[tmp][i]){                 //如果有字符
				in[trie[fail[tmp]][i]]++;            //标记一下fail的入度，方便最后拓扑排序
				fail[trie[tmp][i]]=trie[fail[tmp]][i],op.push_back(trie[tmp][i]);      //根据定义，得出fail数组的转移方程
			}
			else trie[tmp][i]=trie[fail[tmp]][i];        //否则再次转移，但是不添加进队列当中
		} 
	}
}
inline void query(){
	//开始循环遍历文本串
	int p = 0;
	for(i=0;i<temp.size();i++){
		p = trie[p][temp[i]-'a'+1];
		cnt[p]++;         //直接加即可，类似于TAG上的差分
	}
}
inline void topo_sort(){
	//拓扑排序，极大地优化了时间复杂度。
	for(i=0;i<=tot;i++) if(in[i]==0) op.push_back(i);
	while(op.size()){
		int tmp = op.front();
		op.pop_front();
		cnt[fail[tmp]] += cnt[tmp],in[fail[tmp]]--;
		if(in[fail[tmp]]==0) op.push_back(fail[tmp]);
	}
	for(i=0;i<=tot;i++) if(vis[i]) id[vis[i]]=cnt[i];      //标记
}
int main(){
	ios::sync_with_stdio(false);
	cin>>n;
	for(i=1;i<=n;i++) cin>>s[i],add(s[i],i),opp[s[i]]=i;      //用Map标记，可能存在相同的字符串
	build();
	cin>>temp;              //输入文本串
	query();
	topo_sort();
	for(i=1;i<=n;i++) printf("%d\n",id[opp[s[i]]]);        //输出，用Map映射一下编号
	system("pause");
	return 0;
}

fail 树

若 $S$ 在 $T$ 中出现，则 $S$ 一定是 $T$ 的某个前缀的后缀。

我们把每个点的 fail 指针拿出来，恰好就构成了一棵树，这棵树每个节点代表的字符串都是它儿子节点所代表的字符串的最长后缀。

查询 $S$ 在 $T$ 中出现的次数，就是查找有多少个节点是 $T$ 的前缀并且存在一个后缀等于 $S$。

于是就有：如果 $T$ 在遍历字典树的过程中经过的节点的权值都加上 $1$ 的话，模板串 $S$ 出现的次数就是它在 fail 树上代表的节点的子树的权值和。

性质

  1. 某个结点所对应的字符串是它的所有子孙结点所对应的字符串的后缀；

  2. $i$ 的父亲节点对应字符串一定是点 $i$ 对应字符串的最长后缀；

  3. 从点 $i$ 出发往根走，会找到 $i$ 节点的所有后缀节点。即点 $i$ 的祖先一定是点 $i$ 的后缀；

  4. 树上的每个点都是一个单词的前缀，而且每个单词的每个前缀在这棵树上都对应着一个点；

  5. 字符串 $i$ 在自动机里匹配到的每个点在 fail 树上的所有祖先就是 $i$ 的所有子串。

运用

AC 自动机因为是一张有向图，于是就有图上随机游走的问题。

或者是图上 dp/矩阵加速。

这种情况一般都需要理解 AC 自动机每个节点指向的下一个节点一定是当前节点的字符串后面接一个字符，前面砍掉一些字符所代表的节点。

例如 $\text{aabbb}$ 可以转移到 $\texttt{aabbbh}$（如果有），否则就在 $\texttt{abbbh}$，$\texttt{bbbh}$，$\texttt{bbh}$，$\texttt{bh}$，$\texttt{h}$，$\emptyset$ 选存在的较前的元素。

fail 树则通常运用到字符串计数问题里面去，它的性质就是如果 $T$ 在遍历字典树的过程中经过的节点都加上 $1$ 的话，模板串 $S$ 出现的次数就是它在 fail 树上代表的节点的子树的和。