K-D Tree

K-D Tree

二月 10, 2024

K-D Tree

K-D 树存储了 $K$ 维空间下 $n$ 个点的信息，我们可以在树上执行若干操作和若干查询，下面记录了一些常见的用法。

构建

首先给出 K-D 树的一个形态（第一幅图是平面，第二幅图是构建出来的树）：

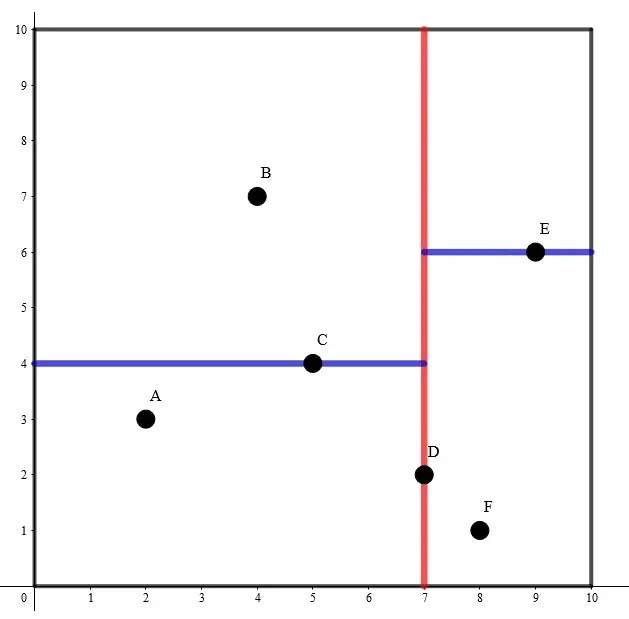
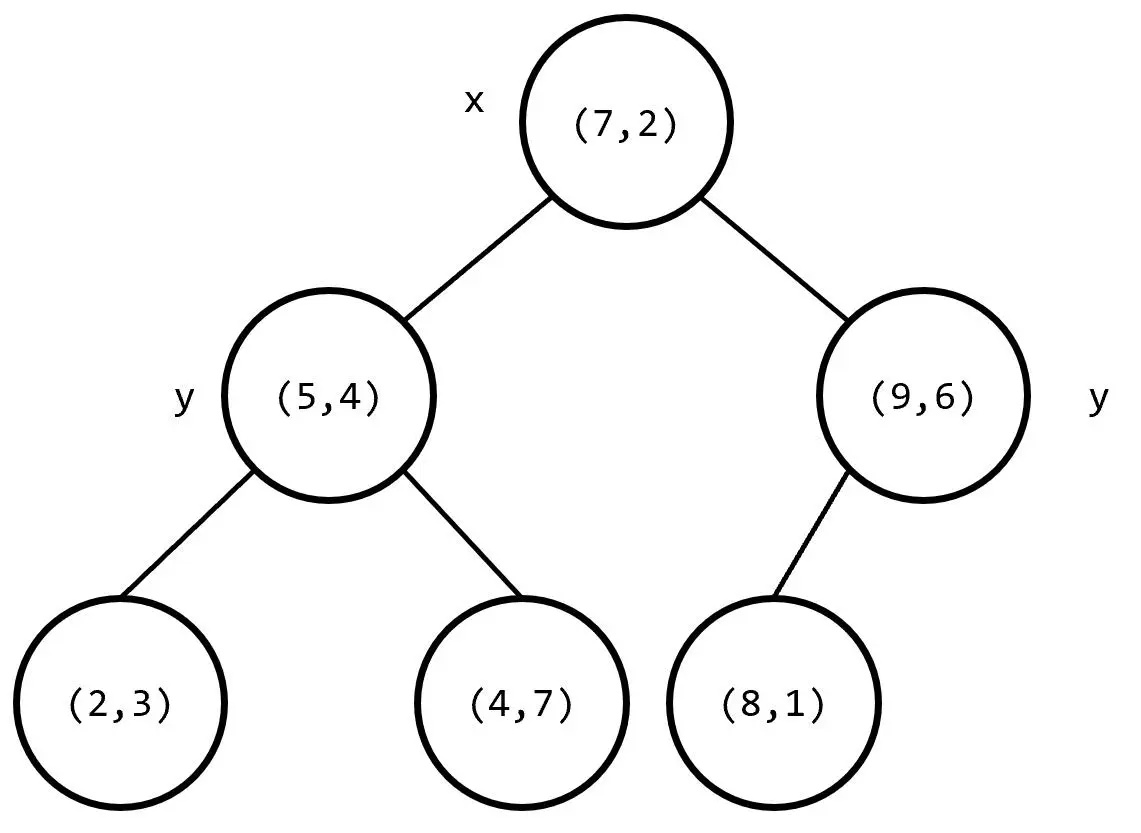
我们发现，对于第 $i$ 个点，我们可以按照 $x$ 坐标排序分成两棵子树，也可以按照 $y$ 坐标排序分成两棵子树，但是为了确保树高，所以一般选取排序之后的中位数作为根节点，然后子树递归建立即可，类似于线段树。

因为要取中位数，所以我们可以通过 sort 选取，或者 nth_element 选取，前一个函数是 $\log$ 的排序，后一个函数是根据排名查找数，是线性的，因此，如果用后者构建的话，时间复杂度是 $O(n \log n)$ 的。

当然，有时候为了减少常数，故选择划分的维度为当前所有维度中方差最大的，这样的话可能会少访问一些点。

建树的代码如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void build(ll l,ll r,ll &p){
	if(l>r) return ;
	if(l==r){
		p=l,tr[p].self=tr[p].maxn=tr[p].minn=d[l];
		return ;
	}
	double p1 = 0,p2 = 0,f1 = 0,f2 = 0;
	for(ll i=l;i<=r;i++) p1+=d[i].x,p2+=d[i].y;
	p1/=(r-l+1),p2/=(r-l+1);
	for(ll i=l;i<=r;i++) f1+=(d[i].x-p1)*(d[i].x-p1),f2+=(d[i].y-p2)*(d[i].y-p2);
	ll mid = (l+r)/2;
	if(f1>f2) nth_element(d+l,d+mid,d+r+1,cmp1),p = mid,tr[p].d = 1,tr[p].self = d[p];
	else nth_element(d+l,d+mid,d+r+1,cmp2),p = mid,tr[p].d = 2,tr[p].self = d[p];
	build(l,mid-1,tr[p].l),build(mid+1,r,tr[p].r);
	pushup(p);
	return ;
}

如果不想用方差的话，当然也可以 $x,y,z,\dots$ 交替选择建树，时间复杂度也不会有太大的影响（邻域查询除外）。’

邻域查询

查找与某个点最接近（或者最远）的点的距离是多少。（曼哈顿距离或者欧拉距离）

为了方便，以下用最接近作为例子，求最远也不难，但是更建议使用凸包。

首先每个节点可以额外维护一个矩形的信息，也就是在它的子树中 $x$ 最小/大是多少，$y$ 最小/大是多少。

当然也可以扩展到 $k$ 维的情况。

每次查询的时候首先判断这个矩形中的点与查找点的最短距离是多少，如果大于当前查询到的答案，直接返回不继续递归了。

否则用根节点所代表的点与查找点的距离更新答案，递归即可。

有一个小优化：

如果左子树的矩形到查找点的最小距离小于右子树的矩形到查找点的最小距离，那么先递归左子树，再递归右子树。

否则先递归右子树，再递归左子树。

时间复杂度

最坏 $O(n)$，但是不失为一种优秀的偏分算法。

期望是在 $O(\sqrt{n})$ 级别的，一般情况下卡不掉，实际可能会被极端数据卡满。

下面是最近点对的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include<bits/stdc++.h>
#define ll long long
#define N 500005
using namespace std;
struct point{ll x,y;}d[N];
point min(point a,point b){return (point){min(a.x,b.x),min(a.y,b.y)};}
point max(point a,point b){return (point){max(a.x,b.x),max(a.y,b.y)};}
bool cmp1(point a,point b){
	if(a.x==b.x) return a.y<b.y;
	return a.x<b.x;
}
bool cmp2(point a,point b){
	if(a.y==b.y) return a.x<b.x;
	return a.y<b.y;
} 
struct tree{
	point self,maxn,minn;
	ll d,l,r;
}tr[N];
ll n,i,root,x,y,ans=LLONG_MAX;
inline void pushup(ll p){
	tr[p].maxn = tr[p].minn = tr[p].self;
	if(tr[p].l) tr[p].maxn = max(tr[p].maxn,tr[tr[p].l].maxn),tr[p].minn = min(tr[p].minn,tr[tr[p].l].minn);
	if(tr[p].r) tr[p].maxn = max(tr[p].maxn,tr[tr[p].r].maxn),tr[p].minn = min(tr[p].minn,tr[tr[p].r].minn);
}
void build(ll l,ll r,ll &p){
	if(l>r) return ;
	if(l==r){
		p=l,tr[p].self=tr[p].maxn=tr[p].minn=d[l];
		return ;
	}
	double p1 = 0,p2 = 0,f1 = 0,f2 = 0;
	for(ll i=l;i<=r;i++) p1+=d[i].x,p2+=d[i].y;
	p1/=(r-l+1),p2/=(r-l+1);
	for(ll i=l;i<=r;i++) f1+=(d[i].x-p1)*(d[i].x-p1),f2+=(d[i].y-p2)*(d[i].y-p2);
	ll mid = (l+r)/2;
	if(f1>f2) nth_element(d+l,d+mid,d+r+1,cmp1),p = mid,tr[p].d = 1,tr[p].self = d[p];
	else nth_element(d+l,d+mid,d+r+1,cmp2),p = mid,tr[p].d = 2,tr[p].self = d[p];
	build(l,mid-1,tr[p].l),build(mid+1,r,tr[p].r);
	pushup(p);
	return ;
}
void solve(ll id,ll x,ll y,ll p){
	if(!p) return ;
	if(p!=id) ans = min(ans,abs(x-tr[p].self.x)*abs(x-tr[p].self.x)+abs(y-tr[p].self.y)*abs(y-tr[p].self.y));
	ll disx = max(tr[p].minn.x-x,x-tr[p].maxn.x),disy = max(tr[p].minn.y-y,y-tr[p].maxn.y);
	disx = max(disx,0ll),disy = max(disy,0ll);
	if(disx*disx+disy*disy>=ans) return ;
	solve(id,x,y,tr[p].l),solve(id,x,y,tr[p].r);
}
int main(){
	ios::sync_with_stdio(false);
	cin>>n;
	for(i=1;i<=n;i++) cin>>d[i].x>>d[i].y;
	build(1,n,root);
	for(i=1;i<=n;i++) solve(i,d[i].x,d[i].y,root);
	cout<<ans<<endl;
	return 0;
}

高维空间的操作

以二维空间为例，我们可以像线段树那样维护可合并信息，即只要提供运算 $+$ 和某个类型 $op$，并且满足 $(a+b)+c=a+(b+c)$ 就可以维护。

例如：矩阵加，矩阵乘，矩阵最大子段和等都可以维护。

我们以基本的矩阵加为例，支持矩阵加和矩阵求和。

首先从根节点开始递归，如果当前节点所记录的矩形与查找的矩形无交集，直接返回。

否则如果当前子树节点都在查找矩形中，打上子树的标记即可。

否则判断根节点在不在查找矩形中，在就打标记，继续递归左右子树查询。

还有，记得 pushdown 和 pushup，其他跟线段树没什么区别。

P6349 [PA2011] Kangaroos 是一道维护最大子段和的题目，可以做一下。

时间复杂度

如果是对于 $k$ 维的空间进行查询和修改，那么时间复杂度经证明是 $O(n^{1-\frac 1k})$ 的。

下面放一下 P6349 的卡常代码和技巧：

  • 尽量用一层成员运算符。

  • 快读快写。

  • 求矩形的时候可以直接 max 函数里面放 $3$ 个参数：自己的，左儿子的，右儿子的，而不是判断有没有左儿子之后再来取 max 或者 min。（$i=0$ 的时候可以先赋 $\text{inf}$ 或者 $-\text{inf}$）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
#include<bits/stdc++.h>
#define inf 1000000000
#define N 200005
using namespace std;
struct point{int x,y,id;}d[N];
struct poly{int l,r,m,x;}emp;
inline poly operator+(poly &a,poly &b){return (poly){max(a.l,(a.l==a.x)*(a.x+b.l)),max(b.r,(b.r==b.x)*(b.x+a.r)),max({a.m,b.m,a.r+b.l}),a.x+b.x};}
point min(point a,point b){return (point){min(a.x,b.x),min(a.y,b.y)};}
point max(point a,point b){return (point){max(a.x,b.x),max(a.y,b.y)};}
bool cmp1(point a,point b){
	if(a.x==b.x) return a.y<b.y;
	return a.x<b.x;
}
bool cmp2(point a,point b){
	if(a.y==b.y) return a.x<b.x;
	return a.y<b.y;
} 
struct tree{
	point self,maxn,minn;
	int d,l,r;
	poly cnt,tag;
}tr[N];
int n,m,i,root,opt,x[N],y[N],ans[N],CNT;
inline void pushup(int p){
	tr[p].maxn = tr[p].minn = tr[p].self = d[p];
	if(tr[p].l) tr[p].maxn = max(tr[p].maxn,tr[tr[p].l].maxn),tr[p].minn = min(tr[p].minn,tr[tr[p].l].minn);
	if(tr[p].r) tr[p].maxn = max(tr[p].maxn,tr[tr[p].r].maxn),tr[p].minn = min(tr[p].minn,tr[tr[p].r].minn);
}
void build(int l,int r,int &p){
	if(l>r) return ;
	if(l==r){
		p=l,tr[p].self=tr[p].maxn=tr[p].minn=d[l];
		return ;
	}
	double p1 = 0,p2 = 0,f1 = 0,f2 = 0;
	for(int i=l;i<=r;i++) p1+=d[i].x,p2+=d[i].y;
	p1/=(r-l+1),p2/=(r-l+1);
	for(int i=l;i<=r;i++) f1+=(d[i].x-p1)*(d[i].x-p1),f2+=(d[i].y-p2)*(d[i].y-p2);
	int mid = (l+r)/2;
	if(f1>f2) nth_element(d+l,d+mid,d+r+1,cmp1),p = mid,tr[p].d = 1,tr[p].self = d[p];
	else nth_element(d+l,d+mid,d+r+1,cmp2),p = mid,tr[p].d = 2,tr[p].self = d[p];
	build(l,mid-1,tr[p].l),build(mid+1,r,tr[p].r);
	pushup(p);
	return ;
}
inline void pushtag(int p,poly a){tr[p].cnt = tr[p].cnt+a,tr[p].tag = tr[p].tag+a;}
inline bool check(int l1,int r1,int l2,int r2,int x,int y){return l1<=x&&x<=r1&&l2<=y&&y<=r2;}
void solve(int l1,int r1,int l2,int r2,int p){
	if(check(l1,r1,l2,r2,tr[p].minn.x,tr[p].minn.y)&&check(l1,r1,l2,r2,tr[p].maxn.x,tr[p].maxn.y)){
		tr[p].cnt.x++,tr[p].cnt.r++,tr[p].cnt.m=max(tr[p].cnt.m,tr[p].cnt.r);
		if(tr[p].cnt.m==tr[p].cnt.x) tr[p].cnt.l++;
		tr[p].tag.x++,tr[p].tag.r++,tr[p].tag.m=max(tr[p].tag.m,tr[p].tag.r);
		if(tr[p].tag.m==tr[p].tag.x) tr[p].tag.l++;
		return ;
	}
	if(tr[p].maxn.y<l2||r2<tr[p].minn.y||tr[p].maxn.x<l1||r1<tr[p].minn.x){
		tr[p].cnt.x++,tr[p].cnt.r=0,tr[p].tag.x++,tr[p].tag.r=0;
		return ;
	}
	if(tr[p].tag.x!=0) pushtag(tr[p].l,tr[p].tag),pushtag(tr[p].r,tr[p].tag),tr[p].tag = emp;
	if(check(l1,r1,l2,r2,tr[p].self.x,tr[p].self.y)) tr[p].cnt.r++,tr[p].cnt.x++,tr[p].cnt.m=max(tr[p].cnt.m,tr[p].cnt.r);
	else tr[p].cnt.r=0,tr[p].cnt.x++;
	if(tr[p].l) solve(l1,r1,l2,r2,tr[p].l);
	if(tr[p].r) solve(l1,r1,l2,r2,tr[p].r);
	return ;
}
void query(int p){
	if(!p) return ;
	pushtag(tr[p].l,tr[p].tag),pushtag(tr[p].r,tr[p].tag),tr[p].tag = emp,ans[tr[p].self.id]=tr[p].cnt.m;
	query(tr[p].l),query(tr[p].r);
}
signed main(){
//	freopen("5.in","r",stdin);
//	freopen("6.out","w",stdout);
	ios::sync_with_stdio(false);
	cin>>n>>m;
	for(i=1;i<=n;i++) cin>>x[i]>>y[i];
	for(i=1;i<=m;i++) cin>>d[i].x>>d[i].y,d[i].id=i;
	build(1,m,root);
	for(i=1;i<=n;i++) solve(1,y[i],x[i],1000000000,root);
	query(root);
	for(i=1;i<=m;i++) cout<<ans[i]<<endl;
	return 0;
}

插入

插入一个节点只需要像平衡树那样找左儿子或者右儿子递归下去查找即可，当找到为空的地方直接传指针新建节点就好。

但是这样会有一个问题，树高不再严格 $O(\log)$，并且每个点不再是它子树内按照某维度排序的中位数，这样的话怎么办呢？

于是我们诞生了两种做法：

万能的：二进制分组，每次插入一个节点到空树里面，然后如果有两棵树的大小相等，就把这两棵树的节点拿出来全部重新构建成一棵新的树，每个节点一定会被合并最多 $\log$ 次，每次合并是 $\log$ 的，因此时间复杂度为 $O(\log^2)$。（例如 AC 自动机就可以这样进行操作）

常数小的：采取替罪羊树的思想，当左（或者右）儿子节点的数量大于等于根节点的节点数量乘上一个阈值（一般是 $0.75$），那么就将这个子树暴力重构。（时间复杂度期望重构约 $\log$ 次）

以下展示 P4169 天使玩偶/SJY摆棋子 的替罪羊树构建版本：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
#include<bits/stdc++.h>
#define N 600005
using namespace std;
struct point{int x,y;}d[N];
point min(point a,point b){return (point){min(a.x,b.x),min(a.y,b.y)};}
point max(point a,point b){return (point){max(a.x,b.x),max(a.y,b.y)};}
bool cmp1(int a,int b){return d[a].x<d[b].x;}
bool cmp2(int a,int b){return d[a].y<d[b].y;} 
struct tree{
	point self,maxn,minn;
	int d,l,r,siz;
}tr[N];
int n,m,i,root,ttt,tot,opt,x,y,ans,l[N],r[N],g[N];
inline void pushup(int p){
	tr[p].maxn = tr[p].minn = tr[p].self = d[p];
	tr[p].siz = tr[tr[p].l].siz + tr[tr[p].r].siz + 1;
	if(tr[p].l) tr[p].maxn = max(tr[p].maxn,tr[tr[p].l].maxn),tr[p].minn = min(tr[p].minn,tr[tr[p].l].minn);
	if(tr[p].r) tr[p].maxn = max(tr[p].maxn,tr[tr[p].r].maxn),tr[p].minn = min(tr[p].minn,tr[tr[p].r].minn);
}
void build(int l,int r,int &p){
	if(l>r){
		p=0;
		return ;
	}
	if(l==r){
		p=g[l],tr[p].self=tr[p].maxn=tr[p].minn=d[g[l]],tr[p].l=tr[p].r=0,tr[p].siz=1;
		return ;
	}
	double p1 = 0,p2 = 0,f1 = 0,f2 = 0;
	for(int i=l;i<=r;i++) p1+=d[g[i]].x,p2+=d[g[i]].y;
	p1/=(r-l+1),p2/=(r-l+1);
	for(int i=l;i<=r;i++) f1+=(d[g[i]].x-p1)*(d[g[i]].x-p1),f2+=(d[g[i]].y-p2)*(d[g[i]].y-p2);
	int mid = (l+r)/2;
	if(f1>f2) nth_element(g+l,g+mid,g+r+1,cmp1),p = g[mid],tr[p].d = 1,tr[p].self = d[p];
	else nth_element(g+l,g+mid,g+r+1,cmp2),p = g[mid],tr[p].d = 2,tr[p].self = d[p];
	build(l,mid-1,tr[p].l),build(mid+1,r,tr[p].r);
	pushup(p);
	return ;
}
inline int get_min(int p,int x,int y){
	if(p==0) return INT_MAX;
	return max({tr[p].minn.x-x,x-tr[p].maxn.x,0})+max({tr[p].minn.y-y,y-tr[p].maxn.y,0});
}
void solve(int x,int y,int p){
	if(!p) return ;
	ans = min(ans,abs(x-tr[p].self.x)+abs(y-tr[p].self.y));
//	cout<<"! "<<x<<" "<<y<<" "<<tr[p].self.x<<" "<<tr[p].self.y<<endl;
	if(get_min(p,x,y)>=ans) return ;
	if(get_min(tr[p].l,x,y)<get_min(tr[p].r,x,y)) solve(x,y,tr[p].l),solve(x,y,tr[p].r);
	else solve(x,y,tr[p].r),solve(x,y,tr[p].l);
}
inline char nc(){
	static char buf[1000000],*p=buf,*q=buf;
	return p==q&&(q=(p=buf)+fread(buf,1,1000000,stdin),p==q)?EOF:*p++;
}
inline int read(){
	int res = 0;
	char c = nc();
	while(c<'0'||c>'9')c=nc();
	while(c<='9'&&c>='0')res=res*10+c-'0',c=nc();
	return res;
}
char obuf[1<<21],*p3=obuf; 
inline void pc(char c){ 
	p3-obuf<=(1<<20)?(*p3++=c):(fwrite(obuf,p3-obuf,1,stdout),p3=obuf,*p3++=c); 
} 
inline void write(int x){ 
	if(x<0) pc('-'),x=-x; 
	if(x>9) write(x/10); 
	pc(x%10+'0'); 
}
void found(int p){
	if(!p) return ;
	g[++ttt] = p;
	found(tr[p].l),found(tr[p].r);
}
void rebuild(int &p){
	ttt=0;
	found(p);
	build(1,ttt,p);
}
inline void insert(int x,int y,int &p){
	if(!p){
		p=++tot,d[tot]=(point){x,y};
		pushup(p);
		return ;
	}
	if(tr[p].d==1){
		if(x<=tr[p].self.x) insert(x,y,tr[p].l);
		else insert(x,y,tr[p].r);
	}
	else{
		if(y<=tr[p].self.y) insert(x,y,tr[p].l);
		else insert(x,y,tr[p].r);
	}
	pushup(p);
	if(tr[p].siz*0.75<=max(tr[tr[p].l].siz,tr[tr[p].r].siz)) rebuild(p);
}
int main(){
//	freopen("1.in","r",stdin);
	n=read(),m=read();
	for(i=1;i<=n;i++) d[i].x=read(),d[i].y=read(),g[i]=i;
	tot=n,ttt=n;
	build(1,ttt,root);
	while(m--){
		opt=read(),x=read(),y=read();
		if(opt==1) insert(x,y,root);
		else{
			ans=INT_MAX;
			solve(x,y,root);
			write(ans),pc('\n');
		}
	}
	fwrite(obuf,p3-obuf,1,stdout);
	return 0;
}

二进制分组版本：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
#include<bits/stdc++.h>
#define N 600005
using namespace std;
struct point{int x,y;}d[N];
point min(point a,point b){return (point){min(a.x,b.x),min(a.y,b.y)};}
point max(point a,point b){return (point){max(a.x,b.x),max(a.y,b.y)};}
bool cmp1(point a,point b){
	if(a.x==b.x) return a.y<b.y;
	return a.x<b.x;
}
bool cmp2(point a,point b){
	if(a.y==b.y) return a.x<b.x;
	return a.y<b.y;
} 
struct tree{
	point self,maxn,minn;
	int d,l,r;
}tr[N];
int n,m,i,root[N],tot,root_tot,opt,x,y,ans,l[N],r[N];
inline void pushup(int p){
	tr[p].maxn = tr[p].minn = tr[p].self;
	if(tr[p].l) tr[p].maxn = max(tr[p].maxn,tr[tr[p].l].maxn),tr[p].minn = min(tr[p].minn,tr[tr[p].l].minn);
	if(tr[p].r) tr[p].maxn = max(tr[p].maxn,tr[tr[p].r].maxn),tr[p].minn = min(tr[p].minn,tr[tr[p].r].minn);
}
void build(int l,int r,int &p){
	if(l>r){
		p=0;
		return ;
	}
	if(l==r){
		p=l,tr[p].self=tr[p].maxn=tr[p].minn=d[l],tr[p].l=tr[p].r=0;
		return ;
	}
	double p1 = 0,p2 = 0,f1 = 0,f2 = 0;
	for(int i=l;i<=r;i++) p1+=d[i].x,p2+=d[i].y;
	p1/=(r-l+1),p2/=(r-l+1);
	for(int i=l;i<=r;i++) f1+=(d[i].x-p1)*(d[i].x-p1),f2+=(d[i].y-p2)*(d[i].y-p2);
	int mid = (l+r)/2;
	if(f1>f2) nth_element(d+l+1,d+mid+1,d+r+1,cmp1),p = mid,tr[p].d = 1,tr[p].self = d[p];
	else nth_element(d+l+1,d+mid+1,d+r+1,cmp2),p = mid,tr[p].d = 2,tr[p].self = d[p];
	build(l,mid-1,tr[p].l),build(mid+1,r,tr[p].r);
	pushup(p);
	return ;
}
inline int get_min(int p,int x,int y){
	if(p==0) return INT_MAX;
	return max({tr[p].minn.x-x,x-tr[p].maxn.x,0})+max({tr[p].minn.y-y,y-tr[p].maxn.y,0});
}
void solve(int x,int y,int p){
	if(!p) return ;
	ans = min(ans,abs(x-tr[p].self.x)+abs(y-tr[p].self.y));
	if(get_min(p,x,y)>=ans) return ;
	if(get_min(tr[p].l,x,y)<get_min(tr[p].r,x,y)) solve(x,y,tr[p].l),solve(x,y,tr[p].r);
	else solve(x,y,tr[p].r),solve(x,y,tr[p].l);
}
inline char nc(){
	static char buf[1000000],*p=buf,*q=buf;
	return p==q&&(q=(p=buf)+fread(buf,1,1000000,stdin),p==q)?EOF:*p++;
}
inline int read(){
	int res = 0;
	char c = nc();
	while(c<'0'||c>'9')c=nc();
	while(c<='9'&&c>='0')res=res*10+c-'0',c=nc();
	return res;
}
char obuf[1<<21],*p3=obuf; 
inline void pc(char c){ 
	p3-obuf<=(1<<20)?(*p3++=c):(fwrite(obuf,p3-obuf,1,stdout),p3=obuf,*p3++=c); 
} 
inline void write(int x){ 
	if(x<0) pc('-'),x=-x; 
	if(x>9) write(x/10); 
	pc(x%10+'0'); 
}
inline void insert(int x,int y){
	d[++tot] = (point){x,y},root_tot++;
	l[root_tot] = r[root_tot] = tot,build(tot,tot,root[root_tot]);
	while(root_tot>=2&&(r[root_tot-1]-l[root_tot-1])==(r[root_tot]-l[root_tot])){
		root_tot--;
		build(l[root_tot],r[root_tot+1],root[root_tot]);
		r[root_tot] = r[root_tot+1];
	}
}
int main(){
	n=read(),m=read();
	for(i=1;i<=n;i++) x=read(),y=read(),insert(x,y);
	while(m--){
		opt=read(),x=read(),y=read();
		if(opt==1) insert(x,y);
		else{
			ans=INT_MAX;
			for(i=1;i<=root_tot;i++) solve(x,y,root[i]);
			write(ans),pc('\n');
		}
	}
	fwrite(obuf,p3-obuf,1,stdout);
	return 0;
}

树套树

树套树就不多说了，常见的是线段树套 K-D Tree，可以参见 P4848 崂山白花蛇草水。

大概就是线段树的每个节点维护一棵 K-D Tree，最后在线段树上二分，二分的过程在 K-D Tree 上查询即可。

修改就暴力替罪羊树重构即可。

时间复杂度 $O(n\sqrt{n}\log n)$，不知道怎么过的。。。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
#include<bits/stdc++.h>
#define N 2600005
using namespace std;
struct tree{int d,l,r,siz,maxnx,minnx,maxny,minny,selfx,selfy;}tr[N];
int n,m,i,root,ttt,tot,opt,x,y,z,k,l,ans,g[N],las,tr_tot,d[N][2];
namespace kdt{
	inline void pushup(int p){
		tr[p].siz = tr[tr[p].l].siz + tr[tr[p].r].siz + 1;
		tr[p].maxny=max({tr[p].selfy,tr[tr[p].l].maxny,tr[tr[p].r].maxny});
		tr[p].maxnx=max({tr[p].selfx,tr[tr[p].l].maxnx,tr[tr[p].r].maxnx});
		tr[p].minny=min({tr[p].selfy,tr[tr[p].l].minny,tr[tr[p].r].minny});
		tr[p].minnx=min({tr[p].selfx,tr[tr[p].l].minnx,tr[tr[p].r].minnx});
	}
	void build(int l,int r,int de,int &p){
		if(l>r){
			p=0;
			return ;
		}
		if(l==r){
			p = g[l],tr[p].l = tr[p].r = 0,tr[p].siz = 1;
			tr[p].maxnx = tr[p].minnx = tr[p].selfx = d[p][0];
			tr[p].maxny = tr[p].minny = tr[p].selfy = d[p][1];
			return ;
		}
		int mid = (l+r)/2;
		nth_element(g+l,g+mid,g+r+1,[&](int a,int b){return d[a][de]<d[b][de];});
		p = g[mid],tr[p].d = de,tr[p].selfx = d[p][0],tr[p].selfy = d[p][1];
		build(l,mid-1,de^1,tr[p].l),build(mid+1,r,de^1,tr[p].r);
		pushup(p);
		return ;
	}
	int solve(int l1,int r1,int l2,int r2,int p){
		if(l1<=tr[p].minnx&&tr[p].minnx<=r1&&l2<=tr[p].minny&&tr[p].minny<=r2&&l1<=tr[p].maxnx&&tr[p].maxnx<=r1&&l2<=tr[p].maxny&&tr[p].maxny<=r2) return tr[p].siz;
		if(tr[p].maxny<l2||r2<tr[p].minny||tr[p].maxnx<l1||r1<tr[p].minnx) return 0;
		int ans = 0;
		if(l1<=tr[p].selfx&&tr[p].selfx<=r1&&l2<=tr[p].selfy&&tr[p].selfy<=r2) ans++;
		if(tr[p].l) ans += solve(l1,r1,l2,r2,tr[p].l);
		if(tr[p].r) ans += solve(l1,r1,l2,r2,tr[p].r);
		return ans;
	}
	void found(int p){
		if(!p) return ;
		g[++ttt] = p,found(tr[p].l),found(tr[p].r);
	}
	void rebuild(int &p,int de){ttt=0,found(p),build(1,ttt,de,p);}
	inline void insert(int x,int y,int de,int &p){
		if(!p){
			p=++tot,tr[p].selfx=d[tot][0]=x,tr[p].selfy=d[tot][1]=y,pushup(p);
			return ;
		}
		if(tr[p].d==0){
			if(x<=tr[p].selfx) insert(x,y,de^1,tr[p].l);
			else insert(x,y,de^1,tr[p].r);
		}
		else{
			if(y<=tr[p].selfy) insert(x,y,de^1,tr[p].l);
			else insert(x,y,de^1,tr[p].r);
		}
		pushup(p);
		if(tr[p].siz>=4&&tr[p].siz*4<max(tr[tr[p].l].siz,tr[tr[p].r].siz)*5) rebuild(p,de);
	}
};
struct node{int l,r,root;}trr[N];
inline char nc(){
	static char buf[1000000],*p=buf,*q=buf;
	return p==q&&(q=(p=buf)+fread(buf,1,1000000,stdin),p==q)?EOF:*p++;
}
inline int read(){
	int res = 0;
	char c = nc();
	while(c<'0'||c>'9')c=nc();
	while(c<='9'&&c>='0')res=res*10+c-'0',c=nc();
	return res;
}
char obuf[1<<21],*p3=obuf; 
inline void pc(char c){ 
	p3-obuf<=(1<<20)?(*p3++=c):(fwrite(obuf,p3-obuf,1,stdout),p3=obuf,*p3++=c); 
} 
inline void write(int x){
	if(x>9) write(x/10);
	pc(x%10^48);
}
void add(int l,int r,int x,int s,int t,int &p){
	if(!p) p=++tr_tot;
	kdt::insert(l,r,0,trr[p].root);
	if(s==t) return ;
	if(x<=(s+t)/2) add(l,r,x,s,(s+t)/2,trr[p].l);
	else add(l,r,x,(s+t)/2+1,t,trr[p].r);
}
int query(int l1,int l2,int r1,int r2,int k,int s,int t,int p){
	if(s==t) return s;
	int temp = kdt::solve(l1,l2,r1,r2,trr[trr[p].r].root);
	if(temp>=k) return query(l1,l2,r1,r2,k,(s+t)/2+1,t,trr[p].r);
	else return query(l1,l2,r1,r2,k-temp,s,(s+t)/2,trr[p].l);
}
int main(){
	tr[0].minnx = tr[0].minny = INT_MAX,tr[0].maxnx = tr[0].maxny = INT_MIN;
	n=read(),m=read();
	while(m--){
		opt=read(),x=read(),y=read();
		x^=las,y^=las;
		if(opt==1){
			z=read(),z^=las;
			add(x,y,z,0,1e9,root);
		}
		else{
			z=read(),k=read(),l=read();
			z^=las,k^=las,l^=las;
			las=query(x,z,y,k,l,0,1e9,root);
			if(las) write(las),pc('\n');
			else pc('N'),pc('A'),pc('I'),pc('V'),pc('E'),pc('!'),pc('O'),pc('R'),pc('Z'),pc('z'),pc('y'),pc('z'),pc('.'),pc('\n');
		}
	}
	fwrite(obuf,p3-obuf,1,stdout);
	return 0;
}