回文自动机（PAM）

回文自动机是一种高效处理回文串相关操作的数据结构，这一节我们专门描述回文自动机以及其扩展应用。

定理：一个字符串中的本质不同回文子串只有 $O(n)$ 个。

证明：考虑 Manacher 的过程，每次复制一个区间暴力扩展是 $O(n)$ 的，而复制的区间的回文串都在之前出现过，所以定理得证。

构建

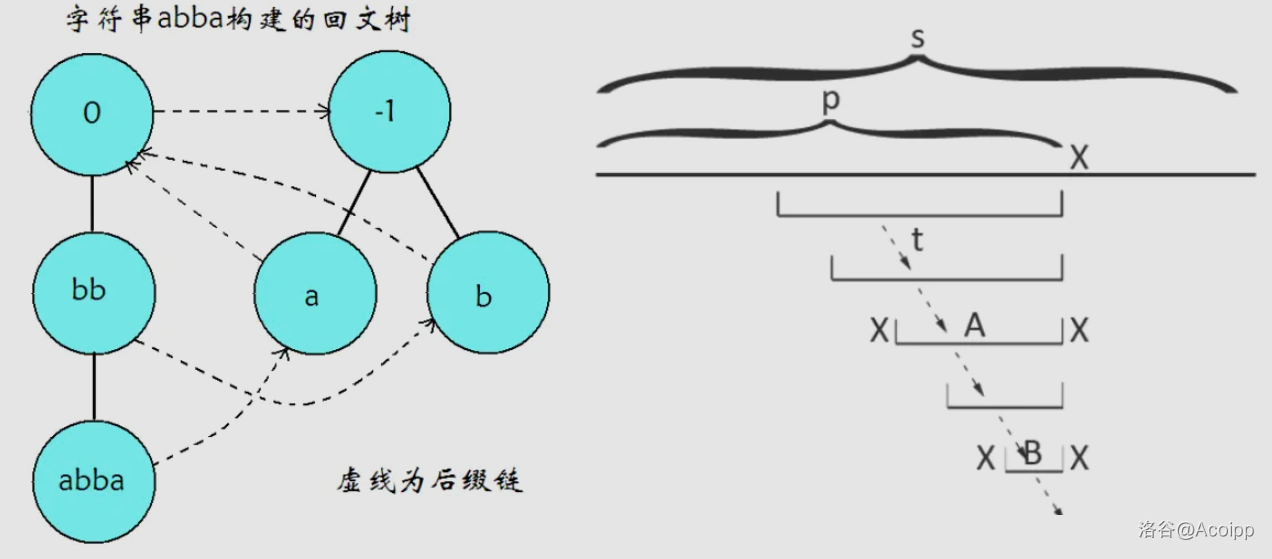
首先，明确一下回文自动机和回文树上的定义：

回文自动机的一个节点 $p$ 代表一个字符串 $S$，从它经过一条转移边 $c$ 到达字符串为 $cSc$ 的节点。

回文树上的一个节点 $p$ 唯一对应回文自动机上的一个节点（双射），$p$ 的父亲 $f_p$ 是 $p$ 所代表字符串的最长回文后缀处在的节点。

任意一个节点都唯一对应一个回文子串，本质相同的回文子串对应相同的节点。

存储的时候，我们只在节点上存储对应回文子串的长度，如果要得知具体的子串，可以记录 endpos 然后递归搜索即可。

于是，我们发现了一个问题，回文子串具有奇数和偶数长度，这两个长度在回文自动机上一定是不相交的，解决方法便是初始状态建立两个根，奇根和偶根，其中偶根在回文树上的父亲是奇根，奇根所代表的字符串长度为 $-1$，偶根代表的字符串长度为 $0$。

考虑加入一个字符 $ch$，回文自动机和回文树会发生什么变化，首先我们需要记录加入之前，这个串的最长回文后缀，这是简单的，然后考虑新的串的最长回文后缀。

设原来的最长回文后缀代表节点为 $p$，那么我们需要顺着 $p$ 在回文树上一直跳转，直到 $p$ 之前的第一个字符等于 $ch$，这个时候，新的串的最长回文后缀就是 $pam_{p,ch}$，特别的，如果没有这个节点，需要新建。

然后考虑新建的节点在回文树上的父亲是什么，然后我们继续顺着 $p$ 在回文树上跳转，直到找到另外一个 $p$ 之前的第一个字符等于 $ch$，这个时候 $pam_{p,ch}$ 就是新建的节点在回文树上的父亲，这个节点是一定存在的，因为它是跳转之前的那个 $p$ 的一个真前缀。

如果找不到，就令新建的节点在回文树上的父亲为偶根，即长度 $0$ 的节点即可，判断是否相等可以判断为 $s_{i-len_p-1}=s_i$，这个时候，奇根也起作用了，因为 $s_{i-(-1)-1}$ 一定等于 $s_i$，所以第一步如果没有匹配上，它就一定会成为奇根的 $pam_{ch}$。

构建过程如下图所示，图片源自 OI-wiki：

时间复杂度：当前节点（最长回文后缀）在回文树上的深度每次最多增加 $1$，所以构建过程为 $O(n)$。

这个回文自动机只支持往后添加字符，考虑如何支持往前添加字符，因为如果 $s$ 是 $t$ 的回文后缀（$t$ 也是回文串），那么 $s$ 也是 $t$ 的回文前缀，所以往前添加字符也可以用这个回文树和回文自动机。

不过需要处理最长回文前缀，注意到在后面添加字符的时候这个东西不会改变；在前面添加字符的时候最长回文后缀也不会改变，除非整个串是回文串，特判一下就可以了。

下面给出支持后端插入的代码，以 P3649 APIO2014 回文串 为例，这道题只需要统计每个回文串出现的次数就可以了，比较简单，套路就是在每个前缀的最长回文后缀那里打一个标记，然后遍历一遍回文树上传标记数量就可以了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

#include<bits/stdc++.h>
#define ll long long
#define N 300005
using namespace std;
char s[N];
ll root_1=1,root0=2,n,i,fath[N],pam[N][26],now=1,tot=2,ne[N],la[N],to[N],et,son[N],ans,len[N];
inline void merge(ll x,ll y){et++,ne[et]=la[x],la[x]=et,to[et]=y;}
inline void insert(ll x,ll id){
	while(s[id]!=s[id-len[now]-1]) now=fath[now];
	if(!pam[now][x]) pam[now][x]=++tot,len[tot]=len[now]+2;
	ll temp = pam[now][x];
	now=fath[now];
	while(now&&s[id]!=s[id-len[now]-1]) now=fath[now];
	if(now) fath[temp]=pam[now][x];
	else fath[temp]=root0;
	now=temp;
}
inline void dfs(ll x){
	for(ll i=la[x];i;i=ne[i]) dfs(to[i]),son[x]+=son[to[i]];
	ans=max(ans,son[x]*len[x]);
}
int main(){
	fath[2]=1,len[1]=-1;
	ios::sync_with_stdio(false);
	cin>>(s+1),n=strlen(s+1);
	for(i=1;i<=n;i++) insert(s[i]-'a',i),son[now]++;
	for(i=2;i<=tot;i++) merge(fath[i],i);
	dfs(1);
	cout<<ans<<endl;
	return 0;
}

其他性质

我们从处理一个串的回文划分数量开始说起。

回文划分，即划分成若干个回文子串的数量，例如 $S=\texttt{abba}$，那么它有 $3$ 种回文划分方式。

暴力统计的话是 $O(n^2)$ 的，我们这里主要讨论的是利用回文后缀的性质的 $O(n \log n)$ 做法。

暴力做法公式：$f_i = \sum_{j=0}^{i-1} f_j p_{j+1,i}$，其中 $p_{l,r}=1/0$ 表示 $S[l,r]$ 是否为回文串。

定理：一个回文串的所有回文后缀可以按照长度划分成 $O(\log n)$ 段。

证明：因为一个回文串的回文后缀一定是这个回文串的 border，问题就变成了一个回文串的 border 可以按照长度划分为 $O(\log n)$ 段，然后用定理“任意字符串的 border 可以按照长度划分成 $O(\log n)$ 段”即可。

于是我们考虑知道了 $f_{1 \sim i-1}$ 的值，添加一个字符之后计算 $f_i$ 的值。

首先我们需要在回文自动机上多维护两个值 $diff_x$ 和 $slink_x$，第一个表示 $len_x-len_{fa_x}$，第二个表示 $x$ 的祖先中离 $x$ 最近的节点满足 $diff_x \ne diff_u$ 的 $u$，此时 $slink_x=u$，根据上面的定理从 $x$ 一直跳 $slink_x$ 可以跳不超过 $\log$ 步到达根节点，这里规定根节点为偶根，奇根只会带来不必要的讨论，故舍弃它。

此外还有一个转移数组 $g_x$ 表示所有 $u \in x \sim slink_x$（不包含 $slink_x$）的 $f_{endpos-len_u}$ 的和，其中 $endpos$ 是 $x$（也是所有 $u$）在原串中出现的最晚的位置。（$x$ 是当前等差数列最长的字符串 $g$ 才有值，否则 $g$ 的值有误）

用图片来表达就是下面这个样子（图片源于 OI-wiki）：

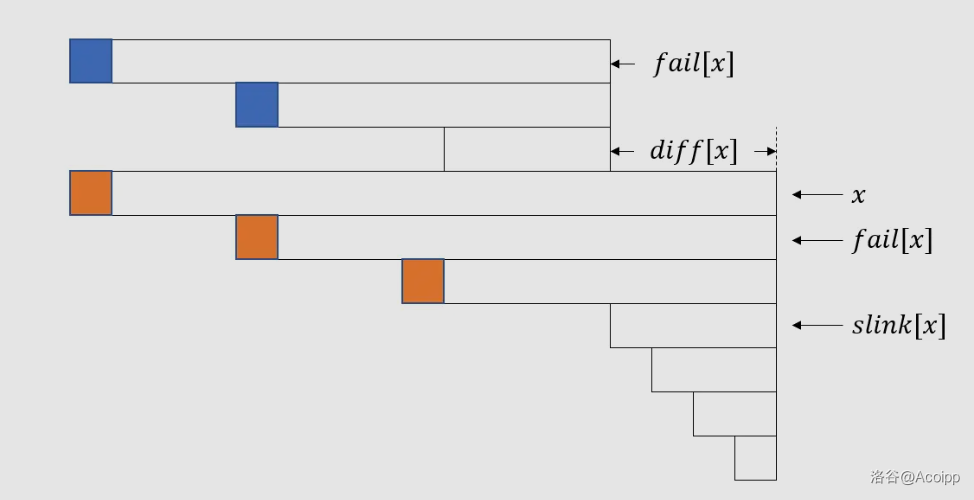
其中 $g_x$ 为所有橙色位置的 $f$ 的和，考虑添加之后如何转移，我们发现添加一个字符之前 $fa_x$ 是其所在等差数列中最长的字符串，否则 $x$ 一定不是所在等差数列中最长的字符串（可以往左扩展 $diff_x$ 步），所以 $g_{fa_x}$ 是正确的，存储了蓝色位置的 $f$ 值，我们发现 $g_x$ 相较于 $g_{fa_x}$ 多了一个 $f_{x-len_{slink_x}-diff_x}$，加上即可。

每次新增一个字符都暴力跳当前最长后缀节点的 $slink$，更新 $g$，然后每次都累加到当前 $f_i$ 中即可，时间复杂度为严格 $O(n \log n)$。

补充说明：建立回文自动机的时候也可以像这样做到单次时间复杂度不超过 $\log$，总和不超过 $O(n)$ 的做法，但是一般不常用，作为技巧积累下来。依据这个性质，还可以完成强制在线的询问区间本质不同回文子串数量，这里就不展开讲了。

例题：Codeforces 932G Palindrome Partition

求 $s_0s_{n-1}s_1s_{n-2}\dots$ 的偶回文划分数，基本上是模板题，只在 $f_i,i \bmod 2=0$ 的地方存储值即可。

下面给出一份参考代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

#include<bits/stdc++.h>
#define ll long long
#define mod 1000000007
#define N 1000005
using namespace std;
char s[N],t[N];
ll root_1=1,root0=2,n,i,j,fath[N],pam[N][26],now=1,tot=2,len[N],dp[N],slink[N],g[N],diff[N];
inline void insert(ll x,ll id){
	while(s[id]!=s[id-len[now]-1]) now=fath[now];
	if(!pam[now][x]) pam[now][x]=++tot,len[tot]=len[now]+2;
	ll temp = pam[now][x];
	now=fath[now];
	while(now&&s[id]!=s[id-len[now]-1]) now=fath[now];
	if(now) fath[temp]=pam[now][x];
	else fath[temp]=root0;
	now=temp,diff[now]=len[now]-len[fath[now]];
	if(diff[now]==diff[fath[now]]) slink[now]=slink[fath[now]];
	else slink[now]=fath[now];
}
int main(){
	fath[2]=1,len[1]=-1,diff[2]=1;
	ios::sync_with_stdio(false);
	cin>>(s+1),n=strlen(s+1);
	for(i=1;i<=n;i++){
		if(i&1) t[i]=s[(i+1)/2];
		else t[i]=s[n-i/2+1];
	}
	for(i=1;i<=n;i++) s[i]=t[i];
	if(n&1){
		cout<<0<<endl;
		return 0;
	}
	dp[0]=1;
	for(i=1;i<=n;i++){
		insert(s[i]-'a',i);
		for(j=now;j>1;j=slink[j]){
			g[j]=dp[i-len[slink[j]]-diff[j]];
			if(diff[j]==diff[fath[j]]) g[j]=(g[j]+g[fath[j]])%mod;
			if(i%2==0) dp[i]=(dp[i]+g[j])%mod;
		}
	}
	cout<<dp[n]<<endl;
	return 0;
}