平衡树
平衡树
本文章中的部分代码和思路来自于 Treap - OI Wiki 和 Splay 树 - OI Wiki。
平衡树是二叉查找树的一种,二叉查找树有一个很强的性质:中序遍历的结果是单调的。
例如下面这棵树:

它的中序遍历就是 $1,2,3,4,5,6,7$,并且树高是 $\log n$,这样的话我们在树上就算暴力跳边,时间复杂度也是 $\log$ 级别的。
但是如果我们是动态插入点的话,就可能会出现一条链的情况,这样的话操作就会退化成 $O(n)$ 级别,如下图所示:
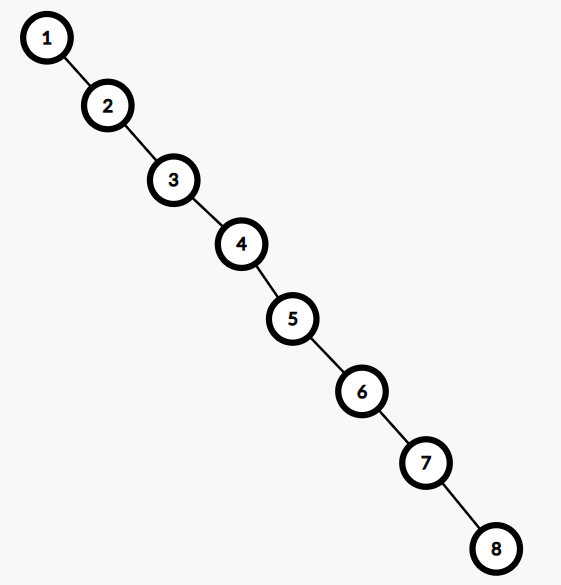
虽然高度是这么大,但是依然满足二叉查找树的性质,于是就有了一个数据结构叫做平衡树,来强制让树高在 $\log$ 级别,此处主要叙述其中一种功能强大,常数小的 Treap。(Splay 请左转 LCT 区)
Treap
平衡树的核心操作就是旋转,因为我们发现同一个中序遍历可以有很多种树的形态,就像上面两张图展示的一样,我们先介绍有旋转的 Treap,再细说一下无旋 Treap(fhq-Treap)。
首先,我们定义左旋为把右儿子节点变到根节点;右旋为把左儿子节点变到根节点。如图所示(节点上的数字是编号,不是权值):
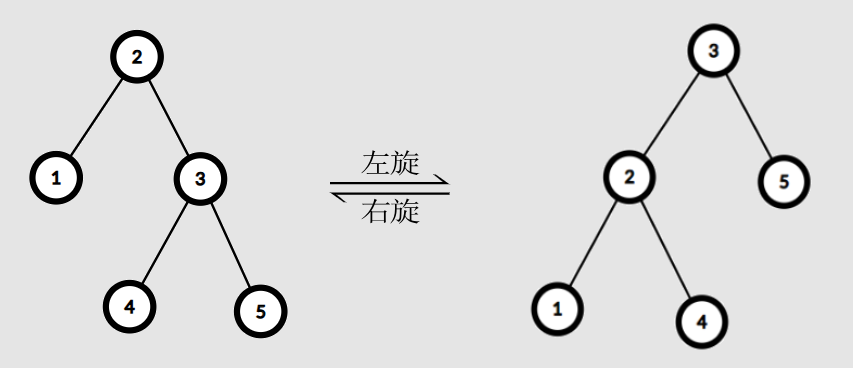
根据平衡树的定义,我们发现这样旋转完全不会影响中序遍历的结果。
于是就有了旋转代码:
1 | void zig(ll &p){ |
其中 zig 是左旋,zag 是右旋。
那什么时候旋转呢?考虑我们学习过的笛卡尔树,它每个节点有两个值,其中一个的中序遍历单调,另外一个则满足堆性质,如果我们给 Treap 上的每个节点给一个堆的键值,如果随机赋值,那么期望高度就是 $O(\log)$ 级别的,这也是 Treap(Tree+heap)名字的由来。
考虑用小根堆的维护,如果父亲节点的堆的键值大于当前节点堆的键值,就往上旋转。(左旋或者右旋视当前节点是父亲的左/右儿子而定)
最后的结果就是这样的:

(第一个值是中序遍历到的值,第二个值是堆的键值)
到现在,平衡树就构建完了,那么我们考虑一下一些基本操作。为了方便起见,可以在树中插入 $-\text{inf}$ 和 $\text{inf}$ 两个值,避免处理边界情况。
插入
直接根据中序遍历的性质查找第一个能够插入的位置就可以了,同时记得更新节点存储的信息和堆的键值,代码如下:
1 | void Insert(ll &p,ll val){ |
删除
跟插入一样,只不过找到节点之后删除需要合并它们的左右子树,分类讨论谁来当父节点就可以:
1 | void Remove(ll &p,ll val){ |
前驱/后继
首先找到当前节点,然后跳左子树即可,如果没有左子树就往父亲节点走,后继同理,不再赘述:
1 | ll gp(ll val){ |
根据值查排名
找到那个值,途中累加经过的点的数量和左子树的数量即可,不难维护:
1 | ll grbv(ll p,ll val){ |
根据排名查值
类似于线段树上二分,如果排名在左子树里面,就跑到左子树里面,否则检查是否等于当前节点,最后跑到右子树里面即可。
1 | ll gvbr(ll p,ll val){ |
综上所述,旋转 Treap 的功能大概就这样,接下来我们介绍一种更强大的平衡树:fhq-treap,它可以维护更多区间的信息,并且更好写。
非旋 Treap
非旋 Treap 的操作只有三个,但是我们可以通过这三个操作实现很多其他的技巧。
分裂-split
这是非旋 Treap 的核心操作,可以看一下下面那幅图,依然来自于 OI-wiki:
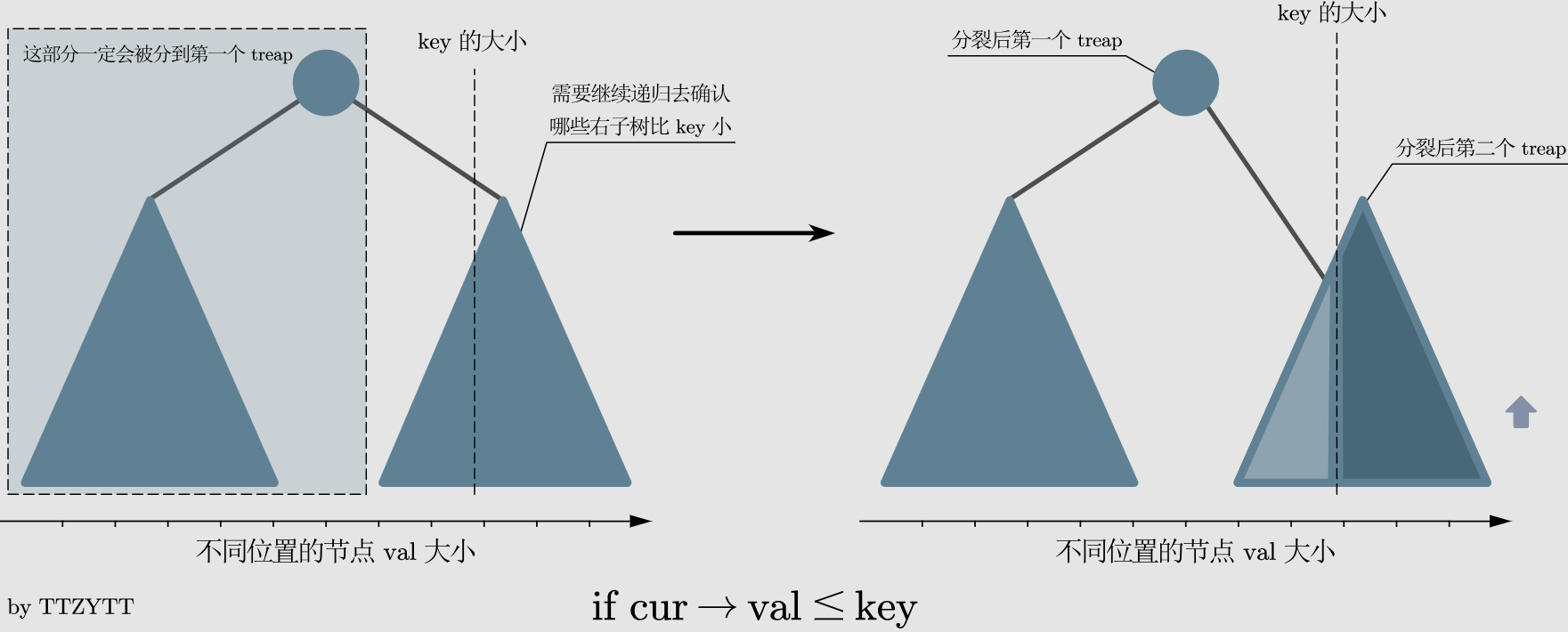
这是按照权值分裂成左右两棵树,当然我们也可以按照树的大小来分裂,后者更为常用,我们可以控制前 $k$ 个元素分裂出来,并且分裂的时间复杂度也是 $O(\log)$ 的。
代码很简单,分类讨论一下根节点是要分裂到左边子树还是右边子树即可:
1 | inline void split(ll x,ll k,ll &p1,ll &p2){ |
合并-merge
按照堆的键值合并两棵子树,像线段树那样合并即可:
1 | inline ll merge(ll p1,ll p2){ |
注意:上面的合并生效当且仅当树上中序遍历不交,即一棵子树中序遍历出来是 $[l,r]$,另外一棵子树中序遍历出来是 $[s,t]$,满足 $r<s$ 才能用上面的函数合并。
那么我们如何处理中序遍历有交的 Treap 合并?于是我们考虑启发式合并的思想,利用如下方法完成合并:
设要合并的两棵树的根节点为 $p_1,p_2$,如果 $siz_{p_1}<siz_{p_2}$,则交换。
然后设 $p_1$ 的树值为 $v_1$,那么把 $p_2$ 分裂成值域为 $[1,v_1-1],[v_1,v_1],[v_1+1,n]$ 三段,然后中间那一段一定只有一个节点,将它与 $p_1$ 这个点合并即可(更新节点的 $cnt$,一个点可能有多个相同权值的点),然后对于剩下两段分别递归求解即可。
边界情况:$p_1=0$ 或者 $p_2=0$ 返回不等于 $0$ 的那一个。
最后这样做的时间复杂度是 $O(\log n)$(merge 函数外没有用 split 函数)或者 $O(\log^2 n)$(merge 函数外使用 split 函数)。下面给出这么做的参考代码:
1 | inline ll merge(ll p1,ll p2){ |
求某个值的排名
像旋转 Treap 那样累加左子树的大小和经过节点的数量即可:
1 | inline ll rankk(ll p,ll k){ |
这三个操作就是非旋转 Treap 的基本操作。
接下来我们考虑用这三个操作处理另外的信息:
插入一个值:找到这个值的排名(小于等于这个值的数量),然后按照排名分裂成两个子树,最后把这个值放到中间合并即可:
1
2
3
4
5
6inline void insert(ll k){
tr[++tot] = (node){0,0,1,k,rnd()};
ll rank = rankk(root,k),r1,r2;
split(root,rank,r1,r2);
root = merge(merge(r1,tot),r2);
}删除一个值:找到这个值的排名(小于等于这个值的数量),然后按照排名分裂成三个子树,最后删去中间的子树,合并其余两棵子树即可:
1
2
3
4inline void erase(ll k){
ll rank = rankk(root,k),r1,r2,r3,tmp;
split(root,rank,r1,r2),split(r1,rank-1,r3,tmp),root=merge(r3,r2);
}查找前驱/后继,找到这个值的排名,然后根据排名找值就可以了,实现很简单:
1
2
3
4
5inline ll find(ll k){ //根据排名找值的函数
ll r1,r2,r3,tmp;
split(root,k,r1,r2),split(r1,k-1,r3,tmp),root=merge(merge(r3,tmp),r2);
return tr[tmp].p;
}
注:无旋 Treap 甚至不需要讨论边界情况,当 $root=0$ 的时候就是边界情况,程序会自动处理。
区间操作
除此之外,非旋 Treap 还支持各种各样的区间操作,下面我们列举几个:
区间翻转
首先,因为非旋 Treap 只有分裂合并操作,没有旋转,区间的 pushdown 和 pushup 比较好实现,就有了区间翻转这个操作。
如果我们想要整体翻转一个二叉树的中序遍历,对于每个节点都翻转左右节点就可以了。
假如说我们要翻转 $[l,r]$ 这个区间,就通过分裂操作分裂成 $[1,l-1]$,$[l,r]$,$[r+1,n]$ 三个区间对应的子树,对于中间那个区间的子树的根打上区间翻转的 tag 即可,同时记得翻转左右子树。
特别注意:split,merge,rank 查询的时候一定要先下放标记,再执行操作,下面附上 P3391 【模板】文艺平衡树 的代码:
1 |
|
区间加/赋值
很简单,不再赘述,套路如线段树下放 tag 那样:
1 | inline void pushtag(ll p,ll c,ll c2){ |
区间维护最大子段和
只需要记住 pushup 的时候更新即可,如果有其它的操作,务必确保操作的先后顺序和操作的合并,下面是有区间赋值/翻转/最大子段和的 pushdown,upd,pushtag 函数:
1 | inline void upd(ll x){ |
Splay
Splay 树一般是学习 Link-Cut Tree 的基础,因为 Splay 的时间复杂度分析需要用到势能分析法,详见 OI-wiki,此处不做展开。
Splay 节点维护的信息约等于 Treap,但是每个节点需要记录当前节点所代表的值有多少个,即 cnt 变量,否则时间复杂度会不对。
基本操作
pushup(x):更新 $x$ 节点以及其子树中的所有信息。
clear(x):销毁 $x$ 节点。
get(x):获取 $x$ 是其父亲的左儿子节点还是有儿子节点。
前两个我们很熟悉,就不讨论了,最后一个是为了后面代码的方便使用,我们规定,如果是左儿子节点返回 $0$,否则返回 $1$,并且使用此函数的时候 $x$ 一定不是 Splay 的根。
扩展操作
旋转
旋转是 Splay 的重点,同 Treap,下面是 Splay 的旋转图:

如果 $x$ 要旋转并且 $x$ 是 $fa_x$ 的左儿子,那么把 $x$ 旋转到根的过程称为右旋,否则称为左旋。
这样旋转不会影响中序遍历的结果,因此我们以右旋为例来看一下如何在代码中实现:
假设需要旋转的节点是 $x$,其父亲为 $y$,在上图中,我们从右往左看,$x=2,y=3$。
- 首先令 $y$ 的左儿子指向 $x$ 的右儿子,如果 $x$ 有右儿子,那么让 $x$ 的右儿子的父亲指向 $y$。
- 然后将 $x$ 的右儿子指向 $y$,并更新 $y$ 的父亲为 $x$,清空 $x$ 的父亲。
- 如果 $y$ 原来有父亲 $z$,如果 $y$ 是 $z$ 的左儿子,那么更新 $z$ 的左儿子为 $x$,$x$ 的父亲为 $z$,反之同理。
左旋是一样的道理,使用位运算就不需要区分左旋还是右旋,代码实现如下:
1 | void rotate(int x) { |
Splay
Splay 操作规定,每次访问了一个节点都要强制把它旋转到根节点,并且在旋转的过程中要尽量保证树高(感性理解一下)。
于是我们有下列三种操作:
ZIG/ZAG
当 $x$ 的父亲 $p$ 是这棵树的根节点的时候,直接沿着 $x-p$ 这条边旋转一次即可,要么 ZIG 要么 ZAG。
ZIG-ZIG/ZAG-ZAG
当 $x$ 和父亲 $p$ 都是它们父亲的左儿子或者右儿子(即 $x-p-q$,$q$ 为 $p$ 的父亲,这三个点构成一条链的时候),需要先沿着 $p-q$ 旋转,再沿着 $x-p$ 旋转,旋转后,这条链就会反向。如果不是这样旋转,那么时间复杂度会出错。
ZIG-ZAG/ZAG-ZIG
最后一种情况,$x$ 和父亲 $p$ 不全是左儿子或者右儿子,那么先旋转 $x-p$,然后 $x$ 和 $p$ 的父亲 $q$ 会生成新的边,最后沿着这条边旋转即可。
写成代码就是下面这个样子:
1 | void splay(int x) { |
插入
插入节点 $x$:
- 树空,直接插入。
- 如果有节点与 $x$ 权值相同,那么令
cnt改变即可。 - 否则按照二叉搜索树的性质找,找到空节点插入即可,最后 Splay。
查询排名/排名为 $x$ 的数
同 Treap,直接在树上通过二叉搜索树的性质找即可。
最后找到了再 Splay 到根。
查询前驱/后继
直接插入 $x$,然后因为这个时候 $x$ 在根节点,所以 $x$ 的前驱是左子树中最后一个节点;后继是右子树中最前面一个节点。
返回答案前记得 Splay 找到的节点到根。
合并两棵 Splay 树
这个操作需要保证值域无交,即一棵树的最大值严格小于另外一棵树的最小值。
- 如果 $x$ 和 $y$ 其中之一或两者都为空树,直接返回不为空的那一棵树的根节点或空树。
- 否则将 $x$ 树中的最大值 Splay 到根,然后把它的右子树设置为 $y$ 并更新节点的信息,然后返回这个节点。
删除
直接把节点 $x$ Splay 到根,然后看 cnt 是否为 $1$,如果不是,直接减去 $1$ 即可,否则合并其左右两棵子树。
其他操作
例如 tag 下放等,需要注意下放的时间以及 pushtag 这个函数里面的边界条件判断,这个东西并不算难,不过细节有的时候有点多。
代码
以洛谷普通平衡树为例,下面展示一下此题代码,时间复杂度为 $O(n \log n)$:
1 |
|
可持久化平衡树
有旋转的平衡树处理可持久化十分困难,于是我们可持久化一般针对于无旋 Treap。
实现起来也很简单,只需要把 split 和 merge 过的所有节点保存下来,因为每次操作是 $\log$ 级别的,空间也是 $\log$ 级别的,最好是能开多大就开多大,因为 Treap 的树高完全取决于随机数。
特别的,如果还有 pushdown 操作的话,pushdown 的时候也要把左右儿子复制一份才行,不然的话会修改到之前的数据。
这里以 P5055【模板】可持久化文艺平衡树 为例介绍:
1 |
|
最后提醒一下,若操作节点编号为 $0$ 请不要操作,因为这是边界情况。
学到这里,才算是真正入门了平衡树。